题目内容
下列的函数是反比例函数的是
- A.y=2x+3
- B.y=x2+2
- C.y=x
- D.
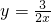
D
分析：根据反比例函数的定义，反比例函数的一般式是y=
（k≠0），可以判定函数的类型．
解答：A、是一次函数，故此选项错误；
B、不是反比例函数，故此选项错误；
C、是正比例函数，故此选项错误；
D、是反比例函数，故此选项正确．
故选D．
点评：本题考查了反比例函数的定义，重点掌握反比例函数的一般式
（k≠0），此一般式可以化为y=kx-1（k≠0）的形式．
分析：根据反比例函数的定义，反比例函数的一般式是y=
（k≠0），可以判定函数的类型．解答：A、是一次函数，故此选项错误；
B、不是反比例函数，故此选项错误；
C、是正比例函数，故此选项错误；
D、是反比例函数，故此选项正确．
故选D．
点评：本题考查了反比例函数的定义，重点掌握反比例函数的一般式
（k≠0），此一般式可以化为y=kx-1（k≠0）的形式． 
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
已知下列命题：
①若a≠b，则a2≠b2；
②对于不为零的实数c，关于x的方程x+
=c+1的根是c．
③对角线互相垂直平分的四边形是菱形．
④过一点有且只有一条直线与已知直线平行．
⑤在反比例函数y=
中，如果函数值y＜1时，那么自变量x＞2，是真命题的个数是 （ ）
①若a≠b，则a2≠b2；
②对于不为零的实数c，关于x的方程x+
| c |
| x |
③对角线互相垂直平分的四边形是菱形．
④过一点有且只有一条直线与已知直线平行．
⑤在反比例函数y=
| 2 |
| x |
| A、4个 | B、3个 | C、2个 | D、1个 |
已知二次函数y=ax2+bx+c（a≠0）自变量x与函数值y之间满足下列数量关系：
（1）观察表中数据，当x=6时，y的值是 ；
（2）这个二次函数与x轴的交点坐标是 ；
（3）代数式
+
+（a+b+c）（a-b+c）的值是 ；
（4）若s、t是两个不相等的实数，当s≤x≤t时，二次函数y=ax2+bx+c（a≠0）有最小值0和最大值24，那么经过点（s+1，t+1）的反比例函数解析式是 ．
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 24 | 15 | 8 | 3 | 0 | -1 | 0 | 3 | 8 | 15 |
（2）这个二次函数与x轴的交点坐标是
（3）代数式
-b+
| ||
| 2a |
-b-
| ||
| 2a |
（4）若s、t是两个不相等的实数，当s≤x≤t时，二次函数y=ax2+bx+c（a≠0）有最小值0和最大值24，那么经过点（s+1，t+1）的反比例函数解析式是
已知正比例函数y1=x，反比例函数
探索研究：