Question

正三角形ABC的边长为1cm，将线段AC绕点A顺时针旋转120°至AP₁，形成扇形D₁；将线段BP₁绕点B顺时针旋转120°至BP₂，形成扇形D₂；将线段CP₂绕点C顺时针旋转120°至CP₃，形成扇形D₃；将线段AP₃绕点A顺时针旋转120°至AP₄，形成扇形D₄；…．试估计n至少为

1.92×10⁹

时扇形D_n的弧长能绕地球赤道一周．（地球赤道半径为6400km，结果用科学记数法表示）

Answer 1

分析：从上图中可以找出规律，弧长的圆心角不变都是120度，变化的是半径，而且第一次是1，第二次是2，第三次是3，依此下去，然后按照弧长公式计算．

解答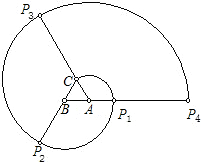：解：由题意得：l₁=

120π×1

180

=

2π

3

；
l₂=

120π×2

180

=

4π

3

；
l₃=

120π×3

180

=2π；
l₄=

120π×4

180

=

8π

3

；
…
l_n=

120π×n

180

；
∵l_n=

120π×n

180

=2π×640000000cm，
∴n=1.92×10⁹．
故答案为：1.92×10⁹．

点评：本题主要考查了弧长公式的实际应用，解答本题一定要理解每一次旋转时的半径，属于规律型题目，注意前面几段弧长的求解，难度一般．