题目内容
在直角坐标系中,△ABC满足,∠C=90°,AC=2,BC=1,点A,C分别在x轴、y轴上,当A点从原点开始在正x轴上运动时,点C随着在正y轴上运动.(1)当A在原点时,求原点O到点B的距离OB;
(2)当OA=OC时,求原点O到点B的距离OB;
(3)求原点O到点B的距离OB的最大值,并确定此时图形应满足什么条件?
分析:(1)根据勾股定理即可求解;
(2)当OA=OC时,如图,△OAC是等腰直角三角形,过点B作BE⊥OA于E,过点C作CD⊥OC,且CD与BE交于点D,再根据两点间的距离公式即可求解;
(3)取AC的中点E,连接OE,BE.在Rt△AOC中,OE是斜边AC上的中线,所以OE=
AC=1.证明当O,E,B在一条直线上时,OB取到最大值时即可求解;
(2)当OA=OC时,如图,△OAC是等腰直角三角形,过点B作BE⊥OA于E,过点C作CD⊥OC,且CD与BE交于点D,再根据两点间的距离公式即可求解;
(3)取AC的中点E,连接OE,BE.在Rt△AOC中,OE是斜边AC上的中线,所以OE=
| 1 |
| 2 |
解答:解:(1)当A点在坐标原点时,如图,
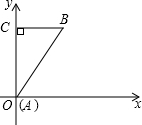
AC在y轴上,BC⊥y轴,
所以OB=
=
.
目的是从特殊情况理解题意,考察勾股定理的基本应用与计算.
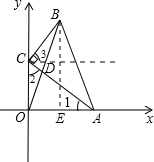
(2)当OA=OC时,如图,△OAC是等腰直角三角形,AC=2.
所以∠1=∠2=45°,OA=OC=
.
过点B作BE⊥OA于E,过点C作CD⊥OC,且CD与BE交于点D,
则∠3=90°-∠ACD=90°-(90°-45°)=45°.又BC=1,
所以CD=BD=
,BE=BD+DE=BD+OC=
,
因此OB=
=
.
(3)解法一:如图所示,设∠ACO=θ,过C作CD⊥OC,
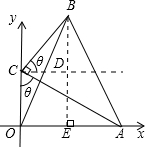
由于∠BCA=90°,所以∠BCD=θ.由AC=2,BC=1,可以得B点的坐标
为B(cosθ,sinθ+2cosθ).则l2=OB2=cos2θ+(sinθ+2cosθ)2=cos2θ+sin2θ+4sinθcosθ+4cos2θ=1+2sin2θ+4cos2θ=3+2sin2θ+2(2cos2θ-1)=3+2sin2θ+2cos2θ=3+2
[
sin2θ+
cos2θ]=3+2
sin(2θ+
)
当θ=
时,l2max=3+2
=(1+
)2,所以lmax=1+
.
解法二:如图,取AC的中点E,连接OE,BE.在Rt△AOC中,OE是斜边AC上的中线,所以OE=
AC=1.
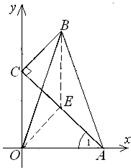
在△ACB中,BC=1,CE=
AC=1,∠BCE=90°,
所以BE=
.
若点O,E,B不在一条直线上,则OB<OE+EB=1+
,
若点O,E,B在一条直线上,
则OB=OE+EB=1+
,
所以当点O,E,B在一条直线上时,OB取到最大值,
最大值是1+
.
当O,E,B在一条直线上时,OB取到最大值时,
从下图可见,OE=1,EB=
.∠CEB=45°,但CE=OE=1,
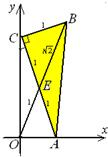 ∠ECO=∠COE=
∠ECO=∠COE=
=
=22.5°.

AC在y轴上,BC⊥y轴,
所以OB=
| AC2+BC2 |
| 5 |
目的是从特殊情况理解题意,考察勾股定理的基本应用与计算.
(2)当OA=OC时,如图,△OAC是等腰直角三角形,AC=2.
所以∠1=∠2=45°,OA=OC=
| 2 |
过点B作BE⊥OA于E,过点C作CD⊥OC,且CD与BE交于点D,
则∠3=90°-∠ACD=90°-(90°-45°)=45°.又BC=1,
所以CD=BD=
| ||
| 2 |
3
| ||
| 2 |
因此OB=
(
|
| 5 |

(3)解法一:如图所示,设∠ACO=θ,过C作CD⊥OC,

由于∠BCA=90°,所以∠BCD=θ.由AC=2,BC=1,可以得B点的坐标
为B(cosθ,sinθ+2cosθ).则l2=OB2=cos2θ+(sinθ+2cosθ)2=cos2θ+sin2θ+4sinθcosθ+4cos2θ=1+2sin2θ+4cos2θ=3+2sin2θ+2(2cos2θ-1)=3+2sin2θ+2cos2θ=3+2
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
当θ=
| π |
| 8 |
| 2 |
| 2 |
| 2 |
解法二:如图,取AC的中点E,连接OE,BE.在Rt△AOC中,OE是斜边AC上的中线,所以OE=
| 1 |
| 2 |

在△ACB中,BC=1,CE=
| 1 |
| 2 |
所以BE=
| 2 |
若点O,E,B不在一条直线上,则OB<OE+EB=1+
| 2 |
若点O,E,B在一条直线上,
则OB=OE+EB=1+
| 2 |
所以当点O,E,B在一条直线上时,OB取到最大值,
最大值是1+
| 2 |
当O,E,B在一条直线上时,OB取到最大值时,
从下图可见,OE=1,EB=
| 2 |
 ∠ECO=∠COE=
∠ECO=∠COE=| ∠CEB |
| 2 |
| 45° |
| 2 |
点评:本题考查了两点间的距离公式及坐标与图形的性质,难度较大,主要是巧妙地利用了线段的基本性质:两点间线段最短.一般地说,线段基本性质常用来求最小值.即线段AB长为定值时,AC+BC的最小值为AB,此时C在AB上.这是线段基本性质的一种应用;而另一种应用往往为人们所忽视:如果两条线段AC和CB在C点接在一起,AC=m与CB=n都是定长;那么AC+BC的最大值为m+n,此时C、A、B三点共线.

练习册系列答案
相关题目
 在直角坐标系中,将坐标为(5,6),(1,2),(3,2),(3,0),(7,0),(7,2),(9,2),(5,6)的点用线段依此连接起来形成一个图案.
在直角坐标系中,将坐标为(5,6),(1,2),(3,2),(3,0),(7,0),(7,2),(9,2),(5,6)的点用线段依此连接起来形成一个图案. 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,