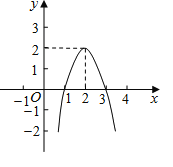题目内容
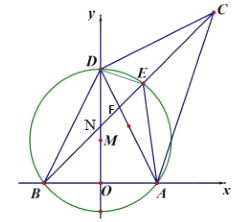
【题目】我们知道:有一内角为直角的三角形叫做直角三角形.类似地我们定义:有一内角为![]() 的三角形叫做半直角三角形.如图,在平面直角坐标系中,
的三角形叫做半直角三角形.如图,在平面直角坐标系中,![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 是
是![]() 轴上的一个动点,
轴上的一个动点,![]() (
(![]() 、
、![]() 、
、![]() 按顺时针方向排列),
按顺时针方向排列),![]() 与经过
与经过![]() 、
、![]() 、
、![]() 三点的
三点的![]() 交于点
交于点![]() ,
,![]() 平分
平分![]() ,连结
,连结![]() ,
,![]() .显然
.显然![]() 、
、![]() 、
、![]() 是半直角三角形.
是半直角三角形.
(1)求证:![]() 是半直角三角形;
是半直角三角形;
(2)求证:![]() ;
;
(3)若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的长;
的长;
(4)![]() 交
交![]() 轴于点
轴于点![]() ,求△ACF与△BCA的面积之比.
,求△ACF与△BCA的面积之比.
【答案】(1)见解析 (2)见解析 (3)见解析 (4)见解析
【解析】
(1)先求得∠ADE=45°,由同弧所对的圆周角可知:∠ABE=∠ADE=45°。根据定义即可得出答案;
(2)根据垂直平分线的性质得:AD=BD,由等角对等边得∠DAB=∠DBA,由D、B、A、E四点共圆,则∠DBA+∠DEA=180°,可得结论;
(3)设圆的半径为r,根据勾股定理可列方程求出r值,由同弧所对的圆心角和圆周角的关系可得∠EMA=2∠ABE=90°,根据勾股定理可得结论;
(4)先证明△ADE≌△CDE,则∠EAC=∠ACE,做辅助线可知:△DGA是等腰直角三角形,由△ACF∽△BCA,由面积比等于相似比即可求出答案。
解:(1)∵∠ADC=90°,DE平分∠ADC,∴∠ADE=45°,∵![]()
![]() 是半直角三角形
是半直角三角形
(2)∵OM⊥AB,OA=OB,
∴AD=BD,
∴∠DAB=∠DBA,
∵∠DEB=∠DAB,
∴∠DBA=∠DEB,
∵D、B、A、E四点共圆,
∴∠DBA+∠DEA=180°,
∵∠DEB+∠DEC=180°,
∴∠DEA=∠DEC
(3)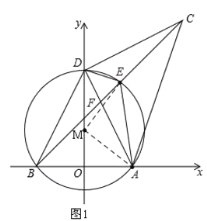
如上图1,连接AM,ME,设![]() 的半径为r
的半径为r
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,
由![]() 得
得![]() 解得
解得![]() ,
,![]() 的半径为
的半径为![]()
∵![]() ,
,
∴∠EMA=2∠ABE=90°
 ,
,
![]()
(4)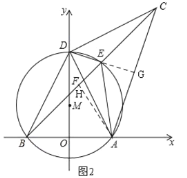
如图2,∵∠ADE=∠CDE=45°,∠DEA=∠DEC,
∴∠DCB=∠DAE
∵∠DAE=∠DBC
∴∠DCB=∠DBC
∴BD=DC=AD
∵DE=DE
∴△ADE≌△CDE
∴AE=CE
∴∠EAC=∠ACE
延长DE交AC于点G,过A作AH⊥BC于H
∴DG⊥AC
∴△DGA是等腰直角三角形
∴∠DAG=45°
∵∠FAC=∠ABC=45°,∠ACB=∠ACF
∴△ACF∽△BCA
∵点D坐标(0,4)
∴OD=4
由勾股定理得AD=![]()
∴AG=![]()
∴AC=2AG=![]()
∵∠ABC=45°,AB=4
∴AH=BH=![]()
由勾股定理得:CH=![]()
∴BC=BH+CH=![]()
∴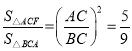

 名校课堂系列答案
名校课堂系列答案