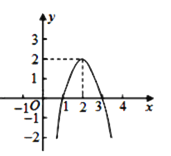Question

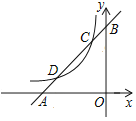
【题目】已知抛物线y＝x2+ax+b与x轴交于点A（﹣1，0），B（3，0）．

（1）求抛物线的解析式；

（2）过点D（0，）作x轴的平行线交抛物线于E，F两点，求EF的长；

（3）当时，直接写出x的取值范围是　 　．

Answer 1

【答案】（1）（2）5；（3）或.

【解析】

（1）把A（-1，0），B（3，0）代入y=x2+ax+b，即可求解；

（2）把点D的纵坐标代入求出x，结合函数图象可得EF的长；

（3）观察函数图象，直线EF上方的部分符合要求，从而得解．

解：（1）把A（-1，0），B（3，0）代入y=x2+ax+b，

得：

解得：

∴抛物线的解析式为；

（2）把y=代入，得

解得：

如图，令E在F左侧，则有，

则EF的长=；

（3）由（2）可知：，

观察图象，当时，直线EF上方的部分符合要求，

∴x的取值范围是或.