Question

如图，兰兰站在河岸上的G点，看见河里有一只小船沿垂直于岸边的方向划过来，此时，测得小船C的俯角是∠FDC=30°，若兰兰的眼睛与地面的距离是1.5米，BG=1米，BG平行于AC所在的直线，迎水坡的坡度i=4：3，坡长AB=10米，求小船C到岸边的距离CA的长？（参考数据：

3

=1.73，结果保留两位有效数字）

Answer 1

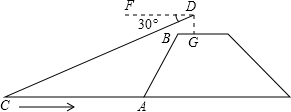
分析：把AB和CD都整理为直角三角形的斜边，利用坡度和勾股定理易得点B和点D到水面的距离，进而利用俯角的正切值可求得CH长度．CH-AE=EH即为AC长度．

解答：解：过点B作BE⊥AC于点E，延长DG交CA于点H，得Rt△ABE和矩形BEHG．
i=

BE

AE

=

4

3

，AB=10，
∴BE=8，AE=6．
∵DG=1.5，BG=1，
∴DH=DG+GH=1.5+8=9.5，
AH=AE+EH=6+1=7．
在Rt△CDH中，
∵∠C=∠FDC=30°，DH=9.5，tan30°=

DH

CH

，
∴CH=9.5

3

．
又∵CH=CA+7，
即9.5

3

=CA+7，
∴CA≈9.435≈9.4（米）．
答：CA的长约是9.4米．

点评：构造所给坡度和所给锐角所在的直角三角形是解决问题的难点，利用坡度和三角函数求值得到相应线段的长度是解决问题的关键．