Question

在矩形ABCD中，M为AD边的中点，P为BC上一点，PE⊥MC，PF⊥MB，当AB、BC满足条件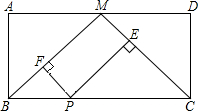

 

时，四边形PEMF为矩形．

Answer 1

分析：根据已知条件、矩形的性质和判定，欲证明四边形PEMF为矩形，只需证明∠BMC=90°，易得AB=

1

2

BC时能满足∠BMC=90°的条件．

解答：解：AB=

1

2

BC时，四边形PEMF是矩形．
∵在矩形ABCD中，M为AD边的中点，AB=

1

2

BC，
∴AB=DC=AM=MD，∠A=∠D=90°，
∴∠ABM=∠MCD=45°，
∴∠BMC=90°，
又∵PE⊥MC，PF⊥MB，
∴∠PFM=∠PEM=90°，
∴四边形PEMF是矩形．

点评：此题考查了矩形的判定和性质的综合应用，是以开放型试题，是中考命题的热点．