题目内容
【题目】一艘轮船位于灯塔P南偏西60°方向的A处，它向东航行20海里到达灯塔P南偏西45°方向上的B处，若轮船继续沿正东方向航行，求轮船航行途中与灯塔P的最短距离．（结果保留根号）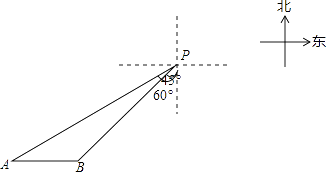
【答案】解：如图，AC⊥PC，∠APC=60°，∠BPC=45°，AP=200，
在Rt△APC中，∵cos∠APC= 
，
∴PC=20cos60°=10，
∴AC= 
=10 
，
在△PBC中，∵∠BPC=45°，
∴△PBC为等腰直角三角形，
∴BC=PC=10，
∴AB=AC﹣BC=10 ﹣10（海里）．
答：轮船航行途中与灯塔P的最短距离是（10 ﹣10）海里．
【解析】利用题意得到AC⊥PC，∠APC=60°，∠BPC=45°，AP=20，如图，在Rt△APC中，利用余弦的定义计算出PC=10，利用勾股定理计算出AC=10 ，再判断△PBC为等腰直角三角形得到BC=PC=10，然后计算AC﹣BC即可．
【考点精析】本题主要考查了关于方向角问题的相关知识点，需要掌握指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角才能正确解答此题．
【题目】中华文明，源远流长；中华汉字，寓意深广．为传承中华优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛．为了解本次大赛的成绩，校团委随机抽取了其中200名学生的成绩作为样本进行统计，制成如下不完整的统计图表：
频数频率分布表
成绩x（分） | 频数（人） | 频率 |
50≤x＜60 | 10 | 0.05 |
60≤x＜70 | 30 | 0.15 |
70≤x＜80 | 40 | n |
80≤x＜90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
根据所给信息，解答下列问题：
（1）m= ， n=；
（2）补全频数分布直方图；
（3）这200名学生成绩的中位数会落在分数段；
（4）若成绩在90分以上（包括90分）为“优”等，请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人？
