题目内容
如图，甲乙两建筑物之间的距离为24m，从甲的顶部C测得建筑物乙底部B的俯角为30°，从甲的顶部测得乙的顶部D的仰角为45°，求两建筑物的高．
解：∵CE⊥BD，
∴∠ABC=∠ECB，
∴AC=AB•tan30°=8
．
∵∠DCE=45°，∴DE=CE•tan45°=24，
∴BD=BE+ED=AC=DE=（24+8）m，
分析：在直角△ABC中，根据AB和∠ABC即可求得AC，在直角△CDE中，根据CE和∠DCE即可求得DE的长，根据BD=BE+ED即可求得BD的长，即可解题．
点评：本题考查了特殊角的三角函数值，考查了三角函数在直角三角形中的运用，本题中计算DE的长是解题的关键．
∴∠ABC=∠ECB，
∴AC=AB•tan30°=8
．∵∠DCE=45°，∴DE=CE•tan45°=24，
∴BD=BE+ED=AC=DE=（24+8
）m，分析：在直角△ABC中，根据AB和∠ABC即可求得AC，在直角△CDE中，根据CE和∠DCE即可求得DE的长，根据BD=BE+ED即可求得BD的长，即可解题．
点评：本题考查了特殊角的三角函数值，考查了三角函数在直角三角形中的运用，本题中计算DE的长是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，甲乙两建筑物之间的距离为24m，从甲的顶部C测得建筑物乙底部B的俯角为30°，从甲的顶部测得乙的顶部D的仰角为45°，求两建筑物的高．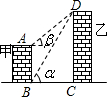
如图，线段AB、DC分别表示甲、乙两建筑物的高．AB⊥BC，DC⊥BC，从B点测得点D的仰角为α，从A点测得点D的仰角为β．已知甲乙两建筑物之间的距离为a，甲建筑物的高AB为
