题目内容
 根据条件求二次函数的解析式:
根据条件求二次函数的解析式:(1)抛物线过(-1,-22),(0,-8),(2,8)三点;
(2)有一个抛物线形拱桥,其最大高度为16m,跨度为40m,现把它的示意图放在平面直角坐标系中如图,求抛物线的解析式.
分析:(1)先设出抛物线的解析式为y=ax2+bx+c,再将点(-1,-22),(0,-8),(2,8)代入解析式中,即可求得抛物线的解析式;
(2)根据题意,抛物线的顶点坐标是(20,16),并且过(0,0),利用抛物线的顶点坐标式待定系数法求它的表达式则可.
(2)根据题意,抛物线的顶点坐标是(20,16),并且过(0,0),利用抛物线的顶点坐标式待定系数法求它的表达式则可.
解答:解:(1)设出抛物线的解析式为y=ax2+bx+c,将点(-1,-22),(0,-8),(2,8)代入解析式得:
,
解得:
,
∴抛物线解析式为:y=-2x2+12x-8;
(2)设y=a(x-20)2+16
因为抛物线过(0,0)
所以代入得:
400a+16=0
即a=-
故此抛物线的函数关系式为:
y=-
(x-20)2+16.
|
解得:
|
∴抛物线解析式为:y=-2x2+12x-8;
(2)设y=a(x-20)2+16
因为抛物线过(0,0)
所以代入得:
400a+16=0
即a=-
| 1 |
| 25 |
故此抛物线的函数关系式为:
y=-
| 1 |
| 25 |
点评:本题考查了用待定系数法求函数表达式的方法,结合图象得出函数图象上点的坐标是解题关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
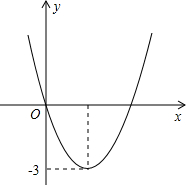 已知,二次函数y=ax2+bx的图象如图所示.
已知,二次函数y=ax2+bx的图象如图所示.