题目内容
 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A(0,4)、B(4,4)、C(6,2)
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A(0,4)、B(4,4)、C(6,2)
(1)用直尺画出该圆弧所在圆的圆心M的位置,并标出M点的坐标;
(2)若D点的坐标为(7,0),验证点D是否在经过点A、B、C的抛物线上;
(3)若D点的坐标为(7,0),想一想直线CD与⊙M有怎样的位置关系,并证明你的猜想.
 解:(1)如图1,点M就是要找的圆心.
解:(1)如图1,点M就是要找的圆心.(2)由A(0,4),可得小正方形的边长为1.设经过点A、B、C的抛物线的解析式为y=ax2+bx+4,依题意有
 ,
,解得,
 ;
;所以经过点A、B、C的抛物线的解析式为y=-
 x2+
x2+ x+4,
x+4,把点D(7,0)的横坐标x=7代入上述解析式,得 y=-
 ×49+
×49+ ×7+4=
×7+4= ≠0,
≠0,所以点D不在经过A、B、C的抛物线上;
(3)证明:由A(0,4),可得小正方形的边长为1.
如图2,设过C点与x轴垂直的直线与x轴的交点为E,连接MC,作直线CD,

∴CE=2,ME=4,ED=1,MD=5,
在Rt△CEM中,∠CEM=90°,
∴MC2=ME2+CE2=42+22=20,
在Rt△CED中,∠CED=90°,
∴CD2=ED2+CE2=12+22=5,
∴MD2=MC2+CD2,
∴∠MCD=90°,
又∵MC为半径,
∴直线CD是⊙M的切线.
分析:(1)题利用“两弦垂直平分线的交点为圆心”可确定圆心位置;
(2)先根据A、B、C三点坐标,用待定系数法求出抛物线的解析式,然后将D点坐标代入抛物线的解析式中,即可判断出点D是否在抛物线的图象上;
(3)由于C在⊙M上,如果CD与⊙M相切,那么C点必为切点;因此可连接MC,证MC是否与CD垂直即可.可根据C、M、D三点坐标,分别表示出△CMD三边的长,然后用勾股定理来判断∠MCD是否为直角.
点评:本题为综合题,涉及圆、平面直角坐标系、二次函数等知识,需灵活运用相关知识解决问题.本题考查二次函数、圆的切线的判定等初中数学的中的重点知识,试题本身就比较富有创新,在网格和坐标系中巧妙地将二次函数与圆的几何证明有机结合,很不错的一道题,令人耳目一新.

练习册系列答案
相关题目
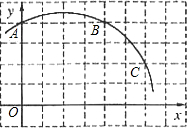 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C. 12、如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( )
12、如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( ) 7、如图,已知直角坐标系中一条圆弧经过正方形网格的格点A,B,C.若A点的坐标为(0,4),D点的坐标为(7,0),那么圆心M点的坐标( )
7、如图,已知直角坐标系中一条圆弧经过正方形网格的格点A,B,C.若A点的坐标为(0,4),D点的坐标为(7,0),那么圆心M点的坐标( )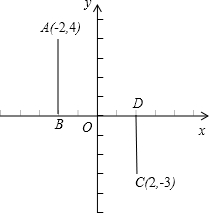 如图,已知直角坐标系中四点A(-2,4),B(-2,0),C(2,-3),D(2,0)、设P是x轴上的点,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,请写出所有符合上述条件的点P的坐标:
如图,已知直角坐标系中四点A(-2,4),B(-2,0),C(2,-3),D(2,0)、设P是x轴上的点,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,请写出所有符合上述条件的点P的坐标: 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.用直尺和圆规画出该圆弧所在圆的圆心M的位置(不用写作法,保留作图痕迹).
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.用直尺和圆规画出该圆弧所在圆的圆心M的位置(不用写作法,保留作图痕迹).