题目内容
如图1,平面直角坐标系xOy中,A,B
.将△OAB绕点O顺时针旋转a角(0°<a<90°)得到△OCD(O,A,B的对应点分别为O,C,D),将△OAB沿
轴负方向平移m个单位得到△EFG(m>0,O,A,B的对应点分别为E,F,G),a,m的值恰使点C,D,F落在同一反比例函数
(k≠0)的图象上.
(1)∠AOB= °,a= °;
(2)求经过点A,B,F的抛物线的解析式;
(3)若(2)中抛物线的顶点为M,抛物线与直线EF的另一个交点为H,抛物线上的点P满足以P,M,F,A为顶点的四边形的面积与四边形MFAH的面积相等(点P不与点H重合),请直接写出满足条件的点P的个数,并求位于直线EF上方的点P的坐标.
.解:(1)∠AOB= 30 °,a= 60 °.…………………………………………………2分
(2)∵ A,B
,△OAB绕点O顺时针旋转a角得到△OCD,(如图7)
∴OA=OB=OC=OD=4.
由(1)得 .
∴ 点C与点A关于x轴对称,点C的坐标为.
∵ 点C,D,F落在同一反比例函数(k≠0)的图象上,
∴ .
∵ 点F是由点A沿轴负方向平移m个单位得到,
∴ ,
,点F的坐标为
.……………3分
∴ 点F与点A关于y轴对称,可设经过点A,B,F的抛物线的解析式为.
∴ 解得
∴ 所求抛物线的解析式为. …………………………………4分
(3)满足条件的点P的个数为 5 .………………………………………………5分
抛物线的顶点为
.
∵ △EFG是由△OAB沿轴负方向平移m个单位得到,
∴ ,
,∠FEG=∠AOB=30°.
∴ 点E的坐标为.
可得直线EF的解析式为.
∵ 点H的横坐标是方程的解,
整理,得.
解得 .
∴ 点H的坐标为.
由抛物线的对称性知符合题意的点的坐标为
.……………6分
可知△AFM是等边三角形,∠MAF= 60°.
由A,M两点的坐标分别为A,
,
可得直线AM的解析式为.
过点H作直线AM的平行线l,设其解析式为(b≠8).
将点H的坐标代入上式,得.
解得,直线l的解析式为
.
∵ 直线l与抛物线的交点的横坐标是方程的解.
整理,得.解得
.
∴ 点满足
,四边形
的面积与四边形MFAH的面积相等.(如图8)……………………………………………7分
点关于y轴的对称点
也符合题意,其坐标为
.………8分
综上所述,位于直线EF上方的点P的坐标分别为,
,
解析:略

 教材全解字词句篇系列答案
教材全解字词句篇系列答案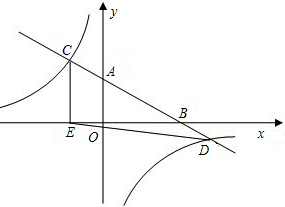 反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=
反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO= M=4,矩形ABCD的边BC在线段OM上,点A、D在抛物线上.
M=4,矩形ABCD的边BC在线段OM上,点A、D在抛物线上. ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP. 如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(8,0),D点坐标为(0,6),则AC长为
如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(8,0),D点坐标为(0,6),则AC长为 如图,在平面直角坐标中,点A(2,2),试在x轴上找点P,使△AOP是等腰三角形,那么这样的三角形有( )
如图,在平面直角坐标中,点A(2,2),试在x轴上找点P,使△AOP是等腰三角形,那么这样的三角形有( )