题目内容
【题目】请阅读下列材料:
问题:已知方程![]() ,求一元二次方程,使它的根分别是已知方程根的2倍.
,求一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为![]() ,则
,则![]() ,所以
,所以![]() .
.
把![]() 代入已知方程,得
代入已知方程,得![]()
化简,得![]()
故所求方程为![]() .
.
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式).
(1)已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为: .
,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为: .
(2)已知关于![]() 的一元二次方程
的一元二次方程![]() 有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数;
有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数;
(3)已知关于![]() 的方程
的方程![]() 有两个实数根,求一个方程,使它的根分别是已知方程根的平方.
有两个实数根,求一个方程,使它的根分别是已知方程根的平方.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)它的根分别是已知方程根的相反数,因此所求方程的根为y,则y=-x,将x=-y代入方程就可得到所求的方程.(2)设所求方程的根为y,可得到x=![]() , 将其代入方程,就可得到a+by+cy2=0,再分情况讨论:当c=0和x≠0,即可求解.(3)设所求方程的根为y,由已知可得到y=x2 , 由此可得到x=
, 将其代入方程,就可得到a+by+cy2=0,再分情况讨论:当c=0和x≠0,即可求解.(3)设所求方程的根为y,由已知可得到y=x2 , 由此可得到x=![]() , 分别将x的值代入方程,就可得到所求的方程.
, 分别将x的值代入方程,就可得到所求的方程.
(1)设所求方程的根为![]() ,则
,则![]() ,
,
所以![]() .
.
把![]() 代入已知方程,得,
代入已知方程,得,![]() ,
,
化简,得![]() ,
,
故所求方程为![]() ;
;
(2)设所求方程的根为![]() ,则
,则![]() ,于是
,于是![]() ,
,
把![]() 代入方程
代入方程![]() ,得
,得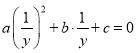 ,
,
去分母,得![]() ,
,
若![]() ,有
,有![]() ,
,
于是方程![]() 有一个根为0,不符合题意,
有一个根为0,不符合题意,
![]() ,
,
故所求方程为![]() ;
;
(3)设所求方程的根为![]() ,则
,则![]() ,
,
所以![]() ,
,
①当![]() 时,把
时,把![]() 代入已知方程,得
代入已知方程,得
![]() ,即
,即![]() ;
;
②当![]() 时,把
时,把![]() 代入已知方程,得
代入已知方程,得
![]() ,即
,即![]()
∴所求方程为![]() 或
或![]() .
.

练习册系列答案
相关题目