题目内容
【题目】如图1，已知
，
平分
．
（1）
；
（2）若在图1中画射线
，设
，
平分
，用含
的代数式表示
的大小；
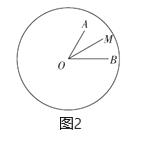
（3）如图2，若线段
与
分别为同一钟表上某一时刻的时针与分针，，在时针与分针转动过程中，始终平分，则经过多少时间后，
的度数第一次等于
．
【答案】（1）
；（2）
或
或
；（3）
.
【解析】
（1）根据角平分线的定义，即可求解；
（2）分3种情况：①当
在
下方时，②当在上方且
时，③当在上方且
时，分别求解即可；
（3）设经过
分钟，
的度数第一次等于
，根据等量关系，列出关于t的方程，即可求解.
（1）∵
，
平分
．
∴
=×60°=.
故答案是：；
（2）①当在下方时，
；
②当在上方且时，
；
③当在上方且时，
；
（3）∵
，平分，
∴
.
设经过分钟，的度数第一次等于，
根据题意得：
，
解得：
∴经过分钟，的度数第一次等于.
练习册系列答案
培优三好生系列答案
相关题目
