题目内容
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.

①求证:△ABE≌△CBD;
②若∠CAE=33°,求∠BDC的度数.
(1)证明见解析;(2)78°.
【解析】
试题分析:①利用SAS即可得证;
②由全等三角形对应角相等得到∠AEB=∠CDB,利用外角的性质求出∠AEB的度数,即可确定出∠BDC的度数.
试题解析:①证明:在△ABE和△CBD中,
 ,
,
∴△ABE≌△CBD(SAS);
②【解析】
∵△ABE≌△CBD,
∴∠AEB=∠BDC,
∵∠AEB为△AEC的外角,
∴∠AEB=∠ACB+∠CAE=33°+45°=78°,
则∠BDC=78°.
考点:1.全等三角形的判定与性质;2.三角形的外角性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




 , -1.314, -17,
, -1.314, -17,  .
. 是单项式
是单项式  是五次单项式
是五次单项式 是四次三项式
是四次三项式  的系数是
的系数是 ,次数是1次
,次数是1次 就可以用下图甲中的面积来说明.
就可以用下图甲中的面积来说明.

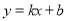 经过第一、二、四象限,则下列正确的是( )
经过第一、二、四象限,则下列正确的是( )