题目内容
 看图填空:
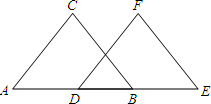
看图填空:已知:如图,BC∥EF,AD=BE,BC=EF,试说明 AC=DF
解:∵AD=BE
∴AD+DB=BE+
DB
DB
(等式的性质)即:AB=
DE
DE
∵BC∥EF
∴∠ABC=∠
DEF
DEF
(两直线平行,同位角相等
两直线平行,同位角相等
)在△ABC和△DEF中
|
∴△ABC≌△DEF(
SAS
SAS
)∴AC=DF (
全等三角形的对应边相等
全等三角形的对应边相等
).分析:由AD=BE可得AB=DE,由BC∥EF得∠ABC=∠DEF,再根据“SAS”判断△ABC≌△DEF,根据全等的性质得到AC=DF.
解答:解:∵AD=BE,
∴AD+DB=BE+DB,
即AB=DE,
∵BC∥EF
∴∠ABC=∠DEF,
∵在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴AC=DF.
故答案为DB;DE;DEF,两直线平行,同位角相等;∠ABC=∠DEF;SAS;全等三角形的对应边相等.
∴AD+DB=BE+DB,
即AB=DE,
∵BC∥EF
∴∠ABC=∠DEF,
∵在△ABC和△DEF中,
|
∴△ABC≌△DEF(SAS),
∴AC=DF.
故答案为DB;DE;DEF,两直线平行,同位角相等;∠ABC=∠DEF;SAS;全等三角形的对应边相等.
点评:本题考查了全等三角形的判定与性质:判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应角相等,对应边相等.

练习册系列答案
相关题目
 23、看图填空:
23、看图填空: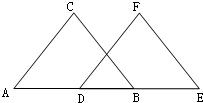 20、看图填空:
20、看图填空: 看图填空:
看图填空:
