题目内容
 已知:如图,在锐角∠MAN的边AN上取一点B,以AB为直径的半圆O交AM于C,交∠MAN的角平分线于E,过点E作ED⊥AM,垂足为D,反向延长ED交AN于F.若cos∠MAN=
已知:如图,在锐角∠MAN的边AN上取一点B,以AB为直径的半圆O交AM于C,交∠MAN的角平分线于E,过点E作ED⊥AM,垂足为D,反向延长ED交AN于F.若cos∠MAN=| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 6 |
| ||
| 2 |
| 1 |
| 6 |
分析:由已知可得到∠MAN=60°,从而推出∠2=∠AFD=30°,根据等角对等边得到EF=AE,再根据S阴=S△OEF-S扇形OEB即可求解.
解答:解:连接OE,
∵cos∠MAN=
,
∴∠MAN=60°.
∴∠2=
∠MAN=
×60°=30°.
∴∠AFD=90°-∠MAN=90°-60°=30°.
∴∠2=∠AFD=∠3=60°,
∴∠OEF=90°,EF=AE=
,
在Rt△OEF中,tan∠OFE=
,
∴tan30°=
.
∴OE=1,
∵∠4=∠2+∠3=60°,
∴S阴=S△OEF-S扇形OEB=
×1×
-
=
-
π.

∵cos∠MAN=
| 1 |
| 2 |
∴∠MAN=60°.
∴∠2=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AFD=90°-∠MAN=90°-60°=30°.
∴∠2=∠AFD=∠3=60°,
∴∠OEF=90°,EF=AE=
| 3 |
在Rt△OEF中,tan∠OFE=
| OE |
| EF |
∴tan30°=
| OE | ||
|
∴OE=1,
∵∠4=∠2+∠3=60°,
∴S阴=S△OEF-S扇形OEB=
| 1 |
| 2 |
| 3 |
| 60π×12 |
| 360 |
| ||
| 2 |
| 1 |
| 6 |
点评:本题考查了扇形的面积计算,解答本题的关键是仔细观察图形,找出不规则图形面积的表示方法,难度一般.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目

 ,AE=
,AE= ,求阴影部分的面积.
,求阴影部分的面积.
 ,AE=
,AE= ,求阴影部分的面积.
,求阴影部分的面积.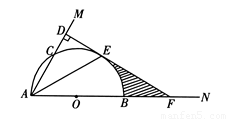
 ,AE=
,AE= ,求阴影部分的面积.
,求阴影部分的面积.