Question

已知：如图，在锐角∠MAN的边AN上取一点B，以AB为直径的半圆O交AM于C，交∠MAN的角平分线于E，过点E作ED⊥AM，垂足为D，反向延长ED交AN于F.

 

 

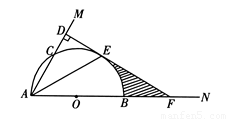
1.猜想ED与⊙O的位置关系，并说明理由；

2.若cos∠MAN=，AE=，求阴影部分的面积.

 

Answer 1

【答案】

 

1.（1）DE与⊙O相切.

理由如下：

连结OE.

 

 

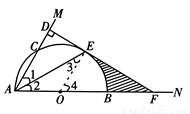
∵AE平分∠MAN,

∴∠1=∠2.

∵OA=OE,

∴∠2=∠3.

∴∠1=∠3,

∴OE∥AD.

∴∠OEF=∠ADF=90°

即OE⊥DE，垂足为E.

又∵点E在半圆O上，

∴ED与⊙O相切.

2.∵cos∠MAN=,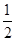

∴∠MAN=60°.

∴∠2=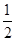∠MAN=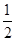×60°=30°,

∠AFD=90°-∠MAN=90°-60°=30°.

∴∠2=∠AFD，

∴EF=AE=.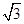

在Rt△OEF中，tan∠OFE=，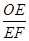

∴tan30°=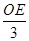，[来源:ZXXK]

∴OE=1.

∵∠4=∠MAN=60°，

∴S阴=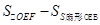

=.

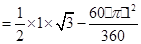
 【解析】略