题目内容
如图1,在△ABC中,AD、BE都是高,两高相交于F.
(1)与△ADC相似的三角形一共有 个;
(2)求证:∠1=∠2;(有两种证法)
(3)如图2,当∠C=60°时,△CDE与△CAB的周长比为 : 、面积比= : .
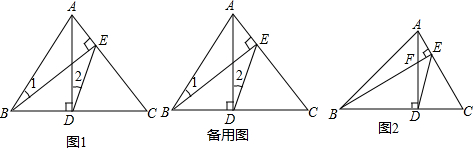
(1)与△ADC相似的三角形一共有
(2)求证:∠1=∠2;(有两种证法)
(3)如图2,当∠C=60°时,△CDE与△CAB的周长比为

考点:相似三角形的判定与性质
专题:
分析:(1)由条件可得∠AFE=∠BFD=∠C,可得到和△ADC相似的有△BEC、△AEF、△BDF共三个;
(2)由△AEF∽△BDF可得到
=
,可证△ABF∽△EDF,可得到∠1=∠2;或由△ADC∽△BEC可得到
=
,即
=
,可知△CDE∽△CAB,可得到∠CDE=∠BAE,再利用条件也可得到∠1=∠2;
(3)由△ADC∽△BEC可得到
=
,即
=
,可知△CDE∽△CAB,且
=
可得出结论.
(2)由△AEF∽△BDF可得到
| AF |
| BF |
| EF |
| DF |
| AC |
| BC |
| CD |
| CE |
| AC |
| CD |
| BC |
| CE |
(3)由△ADC∽△BEC可得到
| AC |
| BC |
| CD |
| CE |
| AC |
| CD |
| BC |
| CE |
| CD |
| AC |
| 1 |
| 2 |
解答:解:(1)∵AD、BE都是高,
∴∠AEF=∠BDF=∠ADC=∠BEC=90°,
∴∠EAF+∠C=∠FBD+∠C=90°,∠AFE+∠BAE=∠BFD+∠FBD=90°,
∴∠AFE=∠BFD=∠C,
∴△ADC∽△BEC∽△AEF∽△BDF,
∴与△ADC相似的三角形有三个,
故答案为:三;
(2)方法一:
∵△AEF∽△BDF
∴
=
,且∠AFE=∠BFD,
∴△ABF∽△EDF,
∴∠1=∠2;
方法二:
∵△ADC∽△BEC,
∴
=
,
∴
=
,且∠ECD=∠ACB,
∴△CDE∽△CAB,
∴∠CDE=∠BAE,
∵∠BAC+∠1=∠CDE+∠2,
∴∠1=∠2;
(3)由(2)可知△CDE∽△CAB,
∵∠C=60°,
∴
=cos60°=
,
∴△CDE和△CAB的周长比为1:2,面积比为1:4,
故答案为:1;2;1;4.
∴∠AEF=∠BDF=∠ADC=∠BEC=90°,
∴∠EAF+∠C=∠FBD+∠C=90°,∠AFE+∠BAE=∠BFD+∠FBD=90°,
∴∠AFE=∠BFD=∠C,
∴△ADC∽△BEC∽△AEF∽△BDF,
∴与△ADC相似的三角形有三个,
故答案为:三;
(2)方法一:
∵△AEF∽△BDF
∴
| AF |
| BF |
| EF |
| DF |
∴△ABF∽△EDF,
∴∠1=∠2;
方法二:
∵△ADC∽△BEC,
∴
| AC |
| BC |
| CD |
| CE |
∴
| AC |
| CD |
| BC |
| CE |
∴△CDE∽△CAB,
∴∠CDE=∠BAE,
∵∠BAC+∠1=∠CDE+∠2,
∴∠1=∠2;
(3)由(2)可知△CDE∽△CAB,
∵∠C=60°,
∴
| CD |
| CA |
| 1 |
| 2 |
∴△CDE和△CAB的周长比为1:2,面积比为1:4,
故答案为:1;2;1;4.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法是解题的关键,注意直角三角形两锐角互余的利用.

练习册系列答案
相关题目
若|a|=5,|b|=1,且a-b<0,则a+b的值等于( )
| A、4或6 | B、4或-6 |
| C、-6或6 | D、-6或-4 |
反比例函数y=-
的图象过点(2,-m),则m的值是( )
| 4 |
| x |
| A、1 | B、2 | C、-2 | D、4 |
下列说法中,错误的是( )
| A、两个全等三角形的对应高相等 |
| B、一条直角边和斜边对应相等的两个直角三角形全等 |
| C、顶角和一腰对应相等的两个等腰三角形全等 |
| D、两角与一边相等的两三角形全等 |
下列命题中,真命题是( )
| A、相等的圆心角所对的弧相等 |
| B、同圆中相等的弦所对的圆周角相等 |
| C、度数相等的弧是等弧 |
| D、相等的圆心角所对的两条弧的度数相等 |

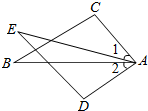 如图,已知∠1=∠2,AC=AD,增加下列条件中能使△ABC≌△AED的条件有( )
如图,已知∠1=∠2,AC=AD,增加下列条件中能使△ABC≌△AED的条件有( )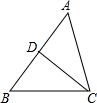 如图,给出下列条件中能够单独判定△ABC∽△ACD的条件的个数为( )
如图,给出下列条件中能够单独判定△ABC∽△ACD的条件的个数为( )