题目内容
 如图△ABC中,∠ACB=90°,CD是高,∠A=30°,求证:BD=
如图△ABC中,∠ACB=90°,CD是高,∠A=30°,求证:BD=| 1 | 4 |
分析:根据直角三角形30°角所对的直角边等于斜边的一半的性质求出BC=
AB,再求出∠BCD=30°,再次利用性质解答即可得证.
| 1 |
| 2 |
解答:证明:∵∠ACB=90°,∠A=30°,
∴BC=
AB,(直角三角形中,30°所对直角边等于斜边的一半),
∵CD是高,
∴∠ADC=90°,
∴∠ACD=60°,
∴∠BCD=30°,
∴BD=
BC,
∴BD=
AB.
∴BC=
| 1 |
| 2 |
∵CD是高,
∴∠ADC=90°,
∴∠ACD=60°,
∴∠BCD=30°,
∴BD=
| 1 |
| 2 |
∴BD=
| 1 |
| 4 |
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,两次利用性质是解题的关键.

练习册系列答案
相关题目
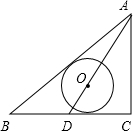 如图△ABC中,∠C=90°,AC=6,AB=10,D是BC边的中点,以AD上一点O为圆心的圆与AB,BC都相切,则⊙O的半径为( )
如图△ABC中,∠C=90°,AC=6,AB=10,D是BC边的中点,以AD上一点O为圆心的圆与AB,BC都相切,则⊙O的半径为( )A、
| ||
B、
| ||
C、
| ||
| D、2 |
 8、如图△ABC中,AB=3,AC=2,BO平分∠ABC,CO平分∠ACB.DE过点O交AB于D,交AC于E,且DE∥BC.则△ADE周长为
8、如图△ABC中,AB=3,AC=2,BO平分∠ABC,CO平分∠ACB.DE过点O交AB于D,交AC于E,且DE∥BC.则△ADE周长为 (2013•南岗区一模)如图△ABC中,DE∥BC,CD、BE交于点F,若DF=1,CF=3,AD=2,则线段BD的长等于
(2013•南岗区一模)如图△ABC中,DE∥BC,CD、BE交于点F,若DF=1,CF=3,AD=2,则线段BD的长等于 如图△ABC中,∠A=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为
如图△ABC中,∠A=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为 如图△ABC中,∠ABC=20°,外角∠ABF的平分线与CA边的延长线交于点D,外角∠EAC的平分线交BC边的延长线于点H,若∠BDA=∠DAB,则∠AHC=( )度.
如图△ABC中,∠ABC=20°,外角∠ABF的平分线与CA边的延长线交于点D,外角∠EAC的平分线交BC边的延长线于点H,若∠BDA=∠DAB,则∠AHC=( )度.