题目内容
 如图,一次函数y=
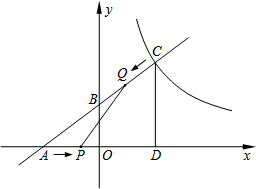
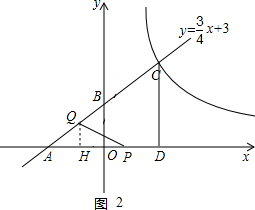
如图,一次函数y= x+m的图象分别交x轴、y轴于点A、B,且与反比例函数y=
x+m的图象分别交x轴、y轴于点A、B,且与反比例函数y=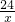 的图象在第一象限交于点C(4,n),CD⊥x轴于D.动点P、Q分别从A、C同时出发,以相同速度沿AD、CA向D、A运动,设AP=k.
的图象在第一象限交于点C(4,n),CD⊥x轴于D.动点P、Q分别从A、C同时出发,以相同速度沿AD、CA向D、A运动,设AP=k.
(1)若△APQ与△AOB相似,求点Q的坐标.
(2)当k为何值时,△APQ为等腰三角形?
(3)是否存在线段PQ将△ACD的面积两等分的k的值?若存在,求出k的值;若不存在,说明理由.
解:(1)∵把(4,n)代入反比例函数y=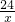 ,得:n=6
,得:n=6
把(4,6)代入一次函数y= x+m,得:m=3
x+m,得:m=3
∴一次函数解析式为:y= x+3.
x+3.
令x=0,则y=3;令y=0,则x=-4.
∴A(-4,0),B(0,3).
∴OA=4,OB=3,AC=10,AB=5,
根据题意,得AP=CQ=k,根据勾股定理,得AC=10,则AQ=10-k
当∠APQ=90°时,△APQ∽△AOB,则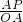 =
=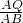 ,即
,即 =
=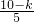 ,解得k=
,解得k=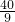 ,
,
∴P( ,0),
,0),
∵点Q在直线AB上,
∴当x= 时,y=
时,y= ×
× +3=
+3= ,
,
∴Q( ,
, );
);
当∠AQP=90°时,△AQP∽△AOB,则有 =
= ,即
,即 =
=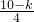 ,k=
,k=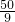 .
.
∴P(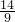 ,0),
,0),
∵点Q在直线AB上,
∴当x=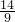 时,y=
时,y= ×
×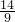 +3=
+3= ,
,
∴Q(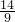 ,
, );
);
(2)①当AP=AQ时,k=10-k,解得,k=5;
②如图1,当PA=PQ时,过点P作PH⊥AB于点H.则易证△AHP∽△AOB,
故有: =
=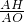 ,即
,即 =
=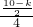 ,解得k=
,解得k= ;
;
③当AQ=PQ时,过点Q作BH⊥AD于点H.则易证△AHQ∽△AOB,故有: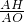 =
=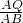 ,即
,即 =
=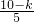 ,解得k=
,解得k=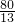 ;
;
综上所述,符合条件的k的值是5, 或
或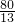 ;
;
(3)不存在线段PQ将△ACD的面积两等分的k的值.理由如下:
△ABC的面积= AC•BC=
AC•BC= ×8×6=24cm2,
×8×6=24cm2,
假设存在t使线段PQ恰好把△ABC的面积平分,
则点Q到AP的距离为:AQ•sin∠A=(10-k)×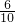 =
= (10-k),
(10-k),
∴△APQ的面积= k•
k• (10-k)=
(10-k)= ×24,
×24,
整理得,k2-10t+40=0,
∵△=(-10)2-4×1×40=-60<0,
∴此方程无解,
∴不存在线段PQ将△ACD的面积两等分的k的值.
分析:(1)首先根据反比例函数的解析式求得n的值,再根据点C的坐标求得m的值.则易求点A、B的坐标;已知△AOB是直角三角形,要使△APQ与△AOB相似,则∠APQ=90°或
∠AQP=90°.根据题意表示对应的两条边,再根据相似三角形的对应边的比相等列方程求解;
(2)根据当AP=AQ时和当PA=PQ时当QA=QP时,分别得出k的值;
(3)先求出△ACD的面积,然后利用∠A的正弦求出点Q到AP的距离,再根据△APQ的面积公式列出方程,然后求出根的判别式△<0,确定不存在.
点评:此题考查了一次函数综合题,其中涉及到了待定系数法求一次函数的解析式,相似三角形的判定与性质;(3)此题运用函数的思想,列出函数表达式,再利用函数列出表达式代入数值进行求解.解答(1)、(2)题时,一定要分类讨论,以防漏解.
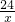 ,得:n=6
,得:n=6把(4,6)代入一次函数y=
 x+m,得:m=3
x+m,得:m=3∴一次函数解析式为:y=
 x+3.
x+3.令x=0,则y=3;令y=0,则x=-4.
∴A(-4,0),B(0,3).
∴OA=4,OB=3,AC=10,AB=5,
根据题意,得AP=CQ=k,根据勾股定理,得AC=10,则AQ=10-k
当∠APQ=90°时,△APQ∽△AOB,则
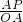 =
=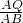 ,即
,即 =
=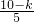 ,解得k=
,解得k=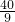 ,
,∴P(
 ,0),
,0),∵点Q在直线AB上,
∴当x=
 时,y=
时,y= ×
× +3=
+3= ,
,∴Q(
 ,
, );
);
当∠AQP=90°时,△AQP∽△AOB,则有
 =
= ,即
,即 =
=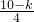 ,k=
,k=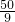 .
.∴P(
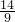 ,0),
,0),∵点Q在直线AB上,
∴当x=
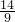 时,y=
时,y= ×
×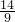 +3=
+3= ,
,∴Q(
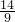 ,
, );
);(2)①当AP=AQ时,k=10-k,解得,k=5;
②如图1,当PA=PQ时,过点P作PH⊥AB于点H.则易证△AHP∽△AOB,
故有:
 =
=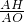 ,即
,即 =
=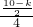 ,解得k=
,解得k= ;
;
③当AQ=PQ时,过点Q作BH⊥AD于点H.则易证△AHQ∽△AOB,故有:
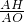 =
=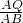 ,即
,即 =
=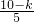 ,解得k=
,解得k=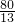 ;
;综上所述,符合条件的k的值是5,
 或
或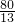 ;
;(3)不存在线段PQ将△ACD的面积两等分的k的值.理由如下:
△ABC的面积=
 AC•BC=
AC•BC= ×8×6=24cm2,
×8×6=24cm2,假设存在t使线段PQ恰好把△ABC的面积平分,
则点Q到AP的距离为:AQ•sin∠A=(10-k)×
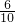 =
= (10-k),
(10-k),∴△APQ的面积=
 k•
k• (10-k)=
(10-k)= ×24,
×24,整理得,k2-10t+40=0,
∵△=(-10)2-4×1×40=-60<0,
∴此方程无解,
∴不存在线段PQ将△ACD的面积两等分的k的值.
分析:(1)首先根据反比例函数的解析式求得n的值,再根据点C的坐标求得m的值.则易求点A、B的坐标;已知△AOB是直角三角形,要使△APQ与△AOB相似,则∠APQ=90°或
∠AQP=90°.根据题意表示对应的两条边,再根据相似三角形的对应边的比相等列方程求解;
(2)根据当AP=AQ时和当PA=PQ时当QA=QP时,分别得出k的值;
(3)先求出△ACD的面积,然后利用∠A的正弦求出点Q到AP的距离,再根据△APQ的面积公式列出方程,然后求出根的判别式△<0,确定不存在.
点评:此题考查了一次函数综合题,其中涉及到了待定系数法求一次函数的解析式,相似三角形的判定与性质;(3)此题运用函数的思想,列出函数表达式,再利用函数列出表达式代入数值进行求解.解答(1)、(2)题时,一定要分类讨论,以防漏解.

练习册系列答案
相关题目
 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y= 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数