题目内容
19.用下列两种边长相同的正多边形不能镶嵌的是( )| A. | 正三角形、正四边形 | B. | 正三角形、正六边形 | ||
| C. | 正四边形、正八边形 | D. | 正三角形、正八边形 |
分析 先计算出正三角形,正四边形,正六边形,正八边形的内角,根据平整镶嵌的条件得出60°和135°不能组成360°,从而得出正三角形和正八边形不可以平整镶嵌.
解答 解:∵正三角形,正四边形,正六边形,正八边形的内角分别为:60°,90°,120°,135°,
∴要用边长相同的两种正多边形材料组合铺设地面,能平整镶嵌必需这两个正多边形的内角的整数倍的和为360°,
∵60°和135°不能组成360°,
∴正三角形和正八边形不能平整镶嵌;
故选D.
点评 本题考查了两个正多边形平整镶嵌的条件:这两个正多边形的内角的整数倍的和为360°,同时也考查了正多边形内角的计算方法.

练习册系列答案
相关题目
7.下列各式计算正确的是( )
| A. | (xy2)3=xy6 | B. | (3ab)2=6a2b2 | C. | (-2x2)2=-4x4 | D. | (a2b3)m=a2mb3m |
11.若a>b,则下列各式正确的是( )
| A. | ac>bc | B. | a2>b2 | C. | -2a<-2b | D. | a-2<b-2 |
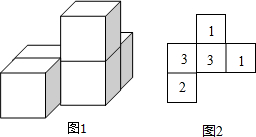 (1)如图1所示,是用五个小正方体搭成的几何体,请画出它的三视图.
(1)如图1所示,是用五个小正方体搭成的几何体,请画出它的三视图.