题目内容
在直角坐标系中，点A（2，0），点B（0，2），则线段AB的中点到原点的距离是（ ）
A、2
| ||
| B、1 | ||
C、
| ||
| D、2 |
考点：两点间的距离公式
专题：
分析：根据点A、B的坐标易求线段AB中点的坐标是（1，1），然后由两点间的距离公式求得该点到原点的距离．
解答：解：∵在直角坐标系中，点A（2，0），点B（0，2），
∴线段AB中点的坐标是（1，1），
∴线段AB的中点到原点的距离是：
=
．
故选：C．
∴线段AB中点的坐标是（1，1），
∴线段AB的中点到原点的距离是：
| 12+12 |
| 2 |
故选：C．
点评：本题考查了两点间的距离公式．求直角坐标系内任意两点间的距离可直接套用此公式．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
平行四边形具有一般四边形不具有的特征是（ ）
| A、外角和为360° |
| B、两条对角线 |
| C、不稳定性 |
| D、对角线互相平分 |
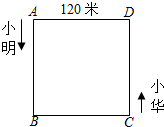如图，正方形的边长为120米，小明和小华都沿着正方形的边按逆时针方向跑步，二人同时起跑，小明从A点开始，速度是4米/秒，小华从C点开始，速度是5.5米/秒，小华第一次追上小明是在边（ ）上．| A、AB | B、BC | C、CD | D、DA |
若一次函数y=-3mx-4（m≠0），当x的值增大时，y的值也增大，则m的取值范围为（ ）
| A、m＞0 | B、m＜0 |
| C、0＜m＜3 | D、无法确定 |
若代数式3-x的值是-2，则x的值是（ ）
| A、5 | B、-5 | C、1 | D、-1 |
函数图象如图，使y＞0相应的x的取值范围是（ ）| A、x＜-3 | B、x＞-3 |
| C、x＜2 | D、x＞2 |
在四边形ABCD中，对角线AC=BD，那么顺次连结四边形ABCD各边的中点所得的四边形一定是（ ）
| A、平行四边形 | B、矩形 |
| C、正方形 | D、菱形 |