题目内容
将抛物线y=x2向下平移后,设它与x轴的两个交点分别为点A,B,且抛物线的顶点为点C.
(1)若△ABC为等边三角形,求此抛物线的函数表达式;
(2)若△ABC为等腰直角三角形,求此抛物线的函数表达式;
(3)若将抛物线改为y=ax2,以上两个问题怎么解答;
(4)若抛物线改为y=a(x-m)2呢?
(5)由此,你发现了什么规律?
(1)若△ABC为等边三角形,求此抛物线的函数表达式;
(2)若△ABC为等腰直角三角形,求此抛物线的函数表达式;
(3)若将抛物线改为y=ax2,以上两个问题怎么解答;
(4)若抛物线改为y=a(x-m)2呢?
(5)由此,你发现了什么规律?
考点:二次函数图象与几何变换
专题:
分析:(1)(2)设抛物线与x轴的左边交点为A,右边交点为B,顶点坐标为(0,-p),然后表示出点A、B的坐标,再根据等边三角形和等腰直角三角形的性质列式计算求出p,即可得解;
(3)(4)思路同上求出点A、B的坐标,再根据等边三角形和等腰直角三角形的性质求解;
(5)根据计算结果解答.
(3)(4)思路同上求出点A、B的坐标,再根据等边三角形和等腰直角三角形的性质求解;
(5)根据计算结果解答.
解答:解:设抛物线与x轴的左边交点为A,右边交点为B,顶点坐标为(0,-p),
则平移后抛物线解析式为y+p=x2,
当y=0时,x=±
,
所以,点A(-
,0),B(
,0),
(1)△ABC为等边三角形,则∠OCA=30°,
所以,OC=
OA,
p=
•
,
解得p=3.
所以,函数解析式为y=x2-3;
(2)△ABC为等腰直角三角形,则∠OCA=45°,
所以,OC=OA,
p=
,
解得p=1,
所以,函数解析式为y=x2-1;
(3)将抛物线改为y=ax2,则平移后抛物线解析式为y+p=ax2,
当y=0时,x=±
,
所以,点A(-
,0),B(
,0),
若△ABC为等边三角形,则∠OCA=30°,
所以,OC=
OA,
p=
•
,
解得p=
,
所以,函数解析式为y=ax2-
;
若△ABC为等腰直角三角形,则∠OCA=45°,
所以,OC=OA,
p=
,
解得p=
,
所以,函数解析式为y=ax2-
;
(4)将抛物线改为y=a(x-m)2,则平移后抛物线解析式为y+p=a(x-m)2,
当y=0时,x=m±
,
所以,点A(m-
,0),B(m+
,0),
若△ABC为等边三角形,则∠OCA=30°,
所以,OC=
OA,
p=
•
,
解得p=
,
所以,函数解析式为y=a(x-m)2-
;
若△ABC为等腰直角三角形,则∠OCA=45°,
所以,OC=OA,
p=
,
解得p=
,
所以,函数解析式为y=a(x-m)2-
;
(5)由计算可知,若△ABC为等边三角形,则平移的距离为
,
若△ABC为等腰直角三角形,则平移距离为
.
则平移后抛物线解析式为y+p=x2,
当y=0时,x=±
| p |
所以,点A(-
| p |
| p |
(1)△ABC为等边三角形,则∠OCA=30°,
所以,OC=
| 3 |
p=
| 3 |
| p |
解得p=3.
所以,函数解析式为y=x2-3;
(2)△ABC为等腰直角三角形,则∠OCA=45°,
所以,OC=OA,
p=
| p |
解得p=1,
所以,函数解析式为y=x2-1;
(3)将抛物线改为y=ax2,则平移后抛物线解析式为y+p=ax2,
当y=0时,x=±
|
所以,点A(-
|
|
若△ABC为等边三角形,则∠OCA=30°,
所以,OC=
| 3 |
p=
| 3 |
|
解得p=
| 3 |
| a |
所以,函数解析式为y=ax2-
| 3 |
| a |
若△ABC为等腰直角三角形,则∠OCA=45°,
所以,OC=OA,
p=
|
解得p=
| 1 |
| a |
所以,函数解析式为y=ax2-
| 1 |
| a |
(4)将抛物线改为y=a(x-m)2,则平移后抛物线解析式为y+p=a(x-m)2,
当y=0时,x=m±
|
所以,点A(m-
|
|
若△ABC为等边三角形,则∠OCA=30°,
所以,OC=
| 3 |
p=
| 3 |
|
解得p=
| 3 |
| a |
所以,函数解析式为y=a(x-m)2-
| 3 |
| a |
若△ABC为等腰直角三角形,则∠OCA=45°,
所以,OC=OA,
p=
|
解得p=
| 1 |
| a |
所以,函数解析式为y=a(x-m)2-
| 1 |
| a |
(5)由计算可知,若△ABC为等边三角形,则平移的距离为
| 3 |
| a |
若△ABC为等腰直角三角形,则平移距离为
| 1 |
| a |
点评:此题主要考查了二次函数的平移规律,熟练利用平移规律得出是解题关键.

练习册系列答案
相关题目
 已知如图,P为△ABC内任意一点,当P在什么位置时PA+PB+PC的值最小?
已知如图,P为△ABC内任意一点,当P在什么位置时PA+PB+PC的值最小?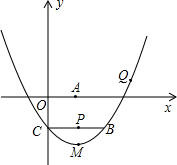 如图,过点C(0,-2)的抛物线y=ax2+bx+c的顶点M坐标为(2,-3),过点C作CB∥x轴交抛物线于点B,点P在线段BC上,CP=m.
如图,过点C(0,-2)的抛物线y=ax2+bx+c的顶点M坐标为(2,-3),过点C作CB∥x轴交抛物线于点B,点P在线段BC上,CP=m. 在△ABC中,∠ABC的平分线BP和外角∠ACD的平分线CP相交于点P,若∠P=30°,求∠A的度数.
在△ABC中,∠ABC的平分线BP和外角∠ACD的平分线CP相交于点P,若∠P=30°,求∠A的度数.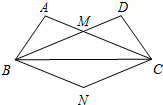 如图,在△ABC和△DCB中,AC=BD,AB=CD,AC、BD交于点M.
如图,在△ABC和△DCB中,AC=BD,AB=CD,AC、BD交于点M.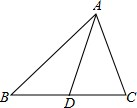 已知:如图△ABC中AD是BC的中线,AB=5cm,AC=3cm,则△ABD和△ACD的周长的差为
已知:如图△ABC中AD是BC的中线,AB=5cm,AC=3cm,则△ABD和△ACD的周长的差为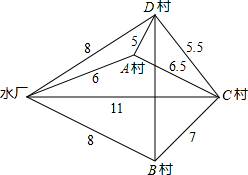 如图,为解决A、B、C、D四个村庄的用水问题,决定在已建水厂与这四个村庄之间铺设供水管道.现在已知这四个村庄及水厂之间的距离(千米).由于地质构造不一样,经测算,在A村和D村之间铺设水管的费用要比其他地方铺设水管的费用每千米增加150%.问:能把水输送到这四个村庄的输水管道成本最省的一条线路的长度是
如图,为解决A、B、C、D四个村庄的用水问题,决定在已建水厂与这四个村庄之间铺设供水管道.现在已知这四个村庄及水厂之间的距离(千米).由于地质构造不一样,经测算,在A村和D村之间铺设水管的费用要比其他地方铺设水管的费用每千米增加150%.问:能把水输送到这四个村庄的输水管道成本最省的一条线路的长度是