Question

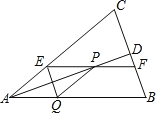
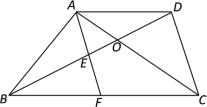
【题目】如图，在梯形ABCD中，AD//BC，AC与BD相交于点O，点E在线段OB上，AE的延长线与BC相交于点F，OD2 = OB·OE．

（1）求证：四边形AFCD是平行四边形；

（2）如果BC=BD，AE·AF=AD·BF，求证：△ABE∽△ACD．

Answer 1

【答案】（1）证明见解析；（2）证明见解析

【解析】

（1）由题意，得到，然后由AD∥BC，得到，则，即可得到AF//CD，即可得到结论；

（2）先证明∠AED=∠BCD，得到∠AEB=∠ADC，然后证明得到，即可得到△ABE∽△ADC.

证明：（1）∵OD2 =OE · OB，

∴．

∵AD//BC，

∴．

∴．

∴ AF//CD．

∴四边形AFCD是平行四边形．

（2）∵AF//CD，

∴∠AED=∠BDC，．

∵BC=BD，

∴BE=BF，∠BDC=∠BCD

∴∠AED=∠BCD．

∵∠AEB=180°∠AED，∠ADC=180°∠BCD，

∴∠AEB=∠ADC．

∵AE·AF=AD·BF，

∴．

∵四边形AFCD是平行四边形，

∴AF=CD．

∴．

∴△ABE∽△ADC．