题目内容
 如图,在正方形ABCD中,对角线AC、BD交于点D,CE平分∠ACD,分别交AD、BD于E、G,EF∥AC交CD于F,连接OE下列结论:①EF=AE,②∠AOE=∠AEO,
如图,在正方形ABCD中,对角线AC、BD交于点D,CE平分∠ACD,分别交AD、BD于E、G,EF∥AC交CD于F,连接OE下列结论:①EF=AE,②∠AOE=∠AEO, ,④S△ACE=2S△DCE,
,④S△ACE=2S△DCE, .其中正确的是
.其中正确的是
- A.①③⑤
- B.①②④
- C.①③④
- D.②③⑤
A
分析:正方形的四个角是直角,对角线垂直相等且平分每一组对角,以及对应线段成比例,勾股定理知识的应用.
解答:∵CE平分∠ACD,EF∥AC,
∴△CFE是等腰三角形,
∴CF=EF,
∵CF=AE,
∴EF=AE.(故①正确).
∵EF≠AO,
∴AE≠AO.(故②错误).

作CA的垂线MA和CE的延长线交于M点,
∵GO= MA,MA=AE,
MA,MA=AE,
∴GO= AE,(故③正确).
AE,(故③正确).

设GO=x,
∵GO= AE=
AE= EF,
EF,
∴EF=AE=2x,
∴DN=NE= EF=x,
EF=x,
∴DE= x,
x,
∵EF∥AC,
∴ =
= ,
,
∴AC=2( +1)x,
+1)x,
∴OD=OA=( +1)x,
+1)x,
∴DG=DO-OG= x,
x,
∵AB=DA=DE+AE= x+2x,
x+2x,
∴AB=( +1)DG.(故⑤正确).
+1)DG.(故⑤正确).
∵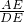 =
= ,
,
∴S△ACE= S△DCE.
S△DCE.
(故④错误).
故正确的为①③⑤.
故选A.
点评:本题考查了正方形的性质,平行线的性质以及勾股定理的知识点.
分析:正方形的四个角是直角,对角线垂直相等且平分每一组对角,以及对应线段成比例,勾股定理知识的应用.
解答:∵CE平分∠ACD,EF∥AC,
∴△CFE是等腰三角形,
∴CF=EF,
∵CF=AE,
∴EF=AE.(故①正确).
∵EF≠AO,
∴AE≠AO.(故②错误).

作CA的垂线MA和CE的延长线交于M点,
∵GO=
 MA,MA=AE,
MA,MA=AE,∴GO=
 AE,(故③正确).
AE,(故③正确).
设GO=x,
∵GO=
 AE=
AE= EF,
EF,∴EF=AE=2x,
∴DN=NE=
 EF=x,
EF=x,∴DE=
 x,
x,∵EF∥AC,
∴
 =
= ,
,∴AC=2(
 +1)x,
+1)x,∴OD=OA=(
 +1)x,
+1)x,∴DG=DO-OG=
 x,
x,∵AB=DA=DE+AE=
 x+2x,
x+2x,∴AB=(
 +1)DG.(故⑤正确).
+1)DG.(故⑤正确).∵
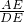 =
= ,
,∴S△ACE=
 S△DCE.
S△DCE.(故④错误).
故正确的为①③⑤.
故选A.
点评:本题考查了正方形的性质,平行线的性质以及勾股定理的知识点.

练习册系列答案
相关题目
 如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比.
如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比. ,交BC于点E.
,交BC于点E. 23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
 如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6