题目内容
如图所示，△ABC中，AD，BE，CF相交于一点，把△ABC分成六个小三角形，图中的数据表示所在的小三角形的面积，则△ABC的面积为________．
315
分析：根据等高不等底的三角形的面积的比等于底边的比，求解，从而不难求得△ABC的面积．
解答：如右图所示，
设S△APE=x，S△BPF=y，
∵S△BDP=40，S△CDP=30，S△CEP=35，
∴
=
=
，
∴
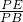=①，
同理可得
=
②，
解关于①②的方程组，得
，
故S△ABC=40+30+35+70+84+56=315．
故答案为315．
点评：本题考查三角形面积的知识，难度不大，关键是设出未知三角形的面积，然后根据等高不等底的三角形的面积的比等于底边的比列式求解．
分析：根据等高不等底的三角形的面积的比等于底边的比，求解，从而不难求得△ABC的面积．
解答：如右图所示，
设S△APE=x，S△BPF=y，
∵S△BDP=40，S△CDP=30，S△CEP=35，
∴
==，∴
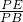=①，同理可得
=②，解关于①②的方程组，得
，故S△ABC=40+30+35+70+84+56=315．
故答案为315．
点评：本题考查三角形面积的知识，难度不大，关键是设出未知三角形的面积，然后根据等高不等底的三角形的面积的比等于底边的比列式求解．
练习册系列答案
名校课堂系列答案
相关题目
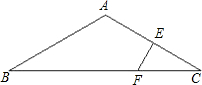如图所示，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．
16、如图所示，△ABC中，∠C=90°，DE垂直平分斜边AB，分别交AB、AC于D、E，∠CAE：∠EAB=5：2，则∠B=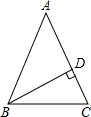
如图所示，△ABC中，AB=AC=10，BD是AC边的高线，DC=2，试求BD的长．
如图所示，△ABC中，BC的垂直平分线交AB于点E，若△ABC的周长为10，BC=4，则△ACE的周长是
如图所示，△ABC中，AB=AC，BD⊥AC，垂足为D，求∠DBC与∠A的关系．