题目内容
因式分解：
（1）4m2+4m3+4m4；
（2）（3x-y）2-（x-3y）2．
（1）4m2+4m3+4m4；
（2）（3x-y）2-（x-3y）2．
考点：提公因式法与公式法的综合运用
专题：
分析：（1）直接提取公因式4m2，进而得出答案；
（2）直接利用平方差公式分解因式得出即可．
（2）直接利用平方差公式分解因式得出即可．
解答：解：（1）4m2+4m3+4m4=4m2（1+m+m2）；
（2）（3x-y）2-（x-3y）2．
=[（3x-y）+（x-3y）][（3x-y）-（x-3y）]
=8（x-y）（x+y）．
（2）（3x-y）2-（x-3y）2．
=[（3x-y）+（x-3y）][（3x-y）-（x-3y）]
=8（x-y）（x+y）．
点评：此题主要考查了提取公因式法以及公式法分解因式，熟练应用平方差公式是解题关键．
练习册系列答案
相关题目
如图所示：∠1=110°，∠2=125°，那么∠3=（ ）| A、55° | B、65° |
| C、75° | D、85° |
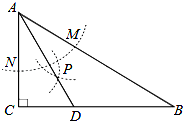如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于（-2）3与-23的值（ ）
| A、互为倒数 | B、互为相反数 |
| C、相等 | D、的和为16 |
如图，在△ABC中，AB=AC=10，BC=7，DE垂直平分AB，交AB于点D，交AC于点E，则△BEC的周长
如图，在长度为1个单位长度的小正方形组成的网格中，点A、B、C在小正方形的顶点上．
如图，已知圆锥底面直径AB=20，母线SA=30．C为母线SB的中点．今有一小虫沿圆锥侧面从A点爬到C点觅食．问它爬过的最短距离应是多少？