题目内容
(2007•贵港)阅读下列材料:一般地,n个相同的因数a相乘a•a•…•a,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为lognb(即lognb).如34=81,则4叫做以3为底81的对数,记为log381(即log381).
请你根据上述材料,计算:log24+log39+log416+log525= .
【答案】分析:根据题目的材料提供的计算方法,计算即可.要注意:22=4,32=9,42=16,52=25.
解答:解:∵22=4,32=9,42=16,52=25.
∴log24=2,log39=2,log416=4,log525=2,
∴log24+log39+log416+log525=2+2+2+2=8.
故答案为:8.
点评:此题考查了学生的阅读能力.解决本题的关键是理解对数的定义,会求对数的值.
解答:解:∵22=4,32=9,42=16,52=25.
∴log24=2,log39=2,log416=4,log525=2,
∴log24+log39+log416+log525=2+2+2+2=8.
故答案为:8.
点评:此题考查了学生的阅读能力.解决本题的关键是理解对数的定义,会求对数的值.

练习册系列答案
相关题目
阅读下表:
解答下列问题:
(1)在上表中空白处分别画出图形,写出结果;
(2)写出线段的总条数N与线段上的点数n的关系式;
(3)试证明:N=
.
| 线段AB上的点数n(包括A、B两点) | 图例 | 线段总条数N |
| 3 |  |
3=2+1 |
| 4 |  |
6=3+2+1 |
| 5 | 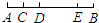 |
10=4+3+2+1 |
| 6 |  |
15=5+4+3+2+1 |
| 7 |
(1)在上表中空白处分别画出图形,写出结果;
(2)写出线段的总条数N与线段上的点数n的关系式;
(3)试证明:N=
| n(n-1) |
| 2 |
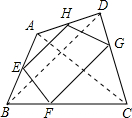 在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的一点,且
在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的一点,且