��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У���֪����AOBC�Ķ���C�������ǣ�2��4��������P�ӵ�A���������߶�AO���յ�O�˶���ͬʱ����Q�ӵ�B���������߶�BC���յ�C�˶�����P��Q���˶��ٶȾ�Ϊ1����λ���˶�ʱ��Ϊt�룮����P��PE��AO��AB�ڵ�E��
��1����ֱ��AB�Ľ���ʽ��
��2�����PEQ�����ΪS����S��tʱ��ĺ�����ϵ����ָ���Ա���t��ȡֵ��Χ��
��3���ڶ���P��Q�˶��Ĺ����У���H�Ǿ���AOBC�ڣ������߽磩һ�㣬����B��Q��E��HΪ������ı��������Σ�ֱ��д��tֵ�������Ӧ�ĵ�H�����꣮
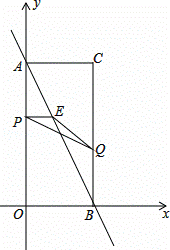
�⣺��1����C��2��4����
��A��0��4����B��2��0����
��ֱ��AB�Ľ���ʽΪy=kx+b��
��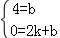 ��
��
���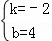
��ֱ��AB�Ľ���ʽΪy=﹣2x+4��
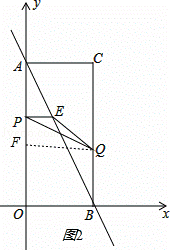
��2����ͼ2������Q��QF��y����F��
��PE��OB��
��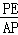 =
=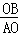 =
=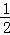
����AP=BQ=t��PE=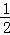 t��AF=CQ=4﹣t��
t��AF=CQ=4﹣t��
��0��t��2ʱ��PF=4﹣2t��
��S= PE•PF=
PE•PF= ��
�� t��4﹣2t��=t﹣
t��4﹣2t��=t﹣ t2��
t2��
��S=﹣ t2+t��0��t��2����
t2+t��0��t��2����
��2��t��4ʱ��PF=2t﹣4��
��S= PE•PF=
PE•PF= ��
�� t��2t﹣4��=
t��2t﹣4��= t2﹣t��2��t��4����
t2﹣t��2��t��4����
��3��t1=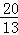 ��H1 ��
��H1 ��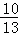 ��
��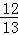 ����
����
t2=20﹣8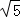 ��H2��10﹣4
��H2��10﹣4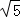 ��4����
��4����

 ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д� ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д���ͼ�ֱ���ij��ȫ��ѧ����ѧʱ�˳������С��ﳵ�����ķֲ�ֱ��ͼ������ͳ��ͼ����ͼ���������������н��۴�����ǣ�������

| �� | A�� | �ð�������Ϊ50�� | B�� | ��������Ϊ30�� |
| �� | C�� | �˳��������ﳵ������2.5�� | D�� | �ﳵ����ռ20% |
��ͼ��һ���ɶ����ͬС�������ɵļ�����ĸ���ͼ��ͼ����������Ϊ��λ��С������ĸ���������������������ͼ�ǣ�������

| �� | A�� |
| B�� |
| C�� |
| D�� |
|
������̰������ѧ�̲���ʹ�õ�ij�ּ��������м��㣬���Ľ��Ϊ��������

| �� | A�� | 21 | B�� | 15 | C�� | 84 | D�� | 67 |
��ͼ��ʾ������ͼ�Σ���������ͼ�ǣ�������

| �� | A�� |
| B�� |
| C�� |
| D�� |
|




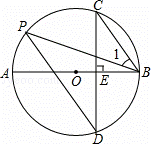
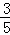 �����O��ֱ����
�����O��ֱ����