题目内容
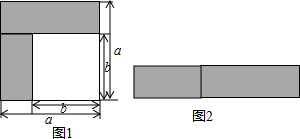
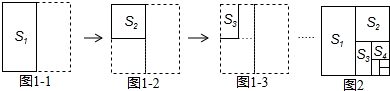
将边长为1的正方形纸片按图1所示方法进行对折，记第1次对折后得到的图形面积为S1，第2次对折后得到的图形面积为S2，…，第n次对折后得到的图形面积为Sn，请根据图2化简，S1+S2+S3+…+S2014= ．
考点：规律型：图形的变化类
专题：规律型
分析：观察图形的变化发现每次折叠后的面积与正方形的关系，从而写出面积和的通项公式．
解答：解：观察发现S1+S2+S3+…+S2014=
+
+
+…+
=1-
，
故答案为：1-
．
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 22014 |
| 1 |
| 22014 |
故答案为：1-
| 1 |
| 22014 |
点评：本题考查了图形的变化类问题，解题的关键是仔细观察图形的变化，并找到图形的变化规律．
练习册系列答案
相关题目
如图，圆心在坐标原点的⊙O的半径为1，若抛物线y=-x2+c和⊙O刚好有三个公共点，则此时c=在平面直角坐标系中，点P（-3，4）关于y轴对称点的坐标为（ ）
| A、（-3，4） |
| B、（3，4） |
| C、（3，-4） |
| D、（-3，-4） |
二次根式
有意义，则x的取值范围是（ ）
| 3-x |
| A、x≤-3 | B、x≥3 |
| C、x≥-3 | D、x≤3 |
以下四组数中，不是勾股数的是（ ）
| A、3，4，5 |
| B、5，12，13 |
| C、4，5，6 |
| D、8，15，17 |
