题目内容
11.计算$\frac{{x}^{2}-4x+4}{2x}$×$\frac{{x}^{2}}{{x}^{2}-2x}$+1,并从0,1,2三个数中选一个合适的数代入求值.分析 把分式的分子分母因式分解,再约分,根据分式有意义的条件,选择x的值,再计算即可.
解答 解:原式=$\frac{(x-2)^{2}}{2x}$•$\frac{{x}^{2}}{x(x-2)}$+1
=$\frac{x-2}{2}$+1
=$\frac{1}{2}$x,
∵2x≠0且x(x-2)≠0,
∴x≠0,2,
∴x=1,
∴原式=$\frac{1}{2}$×1=$\frac{1}{2}$.
点评 本题考查了分式的化简求值,以及分式有意义的条件:分母不为0,掌握分式的通分和约分是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
17.从-$\sqrt{5}$,0,$\sqrt{4}$,π,3.5这五个数中,随机抽取一个,则抽到无理数的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
19.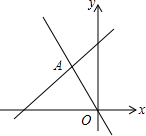 如图,在平面直角坐标系中,直线y=-2x和y=ax+4相交于点A(m,3),则不等式-2x<ax+4的解集为( )
如图,在平面直角坐标系中,直线y=-2x和y=ax+4相交于点A(m,3),则不等式-2x<ax+4的解集为( )
 如图,在平面直角坐标系中,直线y=-2x和y=ax+4相交于点A(m,3),则不等式-2x<ax+4的解集为( )
如图,在平面直角坐标系中,直线y=-2x和y=ax+4相交于点A(m,3),则不等式-2x<ax+4的解集为( )| A. | x<-$\frac{3}{2}$ | B. | x<3 | C. | x>-$\frac{3}{2}$ | D. | x>3 |
16.花卉基地种植了郁金香和玫瑰两种花卉共30亩,设种植郁金香x亩,总收益为y万元,有关数据如表:
(1)求y关于x的函数关系式.(收益=销售额-成本)
(2)若计划投入的总成本不超过70万元,要使获得的总收益最大,基地应种植郁金香和玫瑰各多少亩?
(3)已知郁金香每亩地需要化肥400kg,玫瑰每亩地需要化肥600kg.根据(2)中的种植亩数,某地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的1.25倍,结果运送完全部化肥的次数比原计划少1次,求基地原计划每次运送化肥多少千克?
| 成本 (单位:万元/亩) | 销售额(单位:万元/亩) | |
| 郁金香 | 2.4 | 3 |
| 玫瑰 | 2 | 2.5 |
(2)若计划投入的总成本不超过70万元,要使获得的总收益最大,基地应种植郁金香和玫瑰各多少亩?
(3)已知郁金香每亩地需要化肥400kg,玫瑰每亩地需要化肥600kg.根据(2)中的种植亩数,某地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的1.25倍,结果运送完全部化肥的次数比原计划少1次,求基地原计划每次运送化肥多少千克?
3.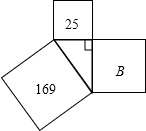 如图,以直角三角形的三边作三个正方形,已知图中两个正方形的面积分别为169,25,则字母B所代表的正方形的面积是( )
如图,以直角三角形的三边作三个正方形,已知图中两个正方形的面积分别为169,25,则字母B所代表的正方形的面积是( )
 如图,以直角三角形的三边作三个正方形,已知图中两个正方形的面积分别为169,25,则字母B所代表的正方形的面积是( )
如图,以直角三角形的三边作三个正方形,已知图中两个正方形的面积分别为169,25,则字母B所代表的正方形的面积是( )| A. | 144 | B. | 194 | C. | 12 | D. | 169 |
 如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-3分别与x轴、y轴交于点A、B,点P的坐标为(0,4).若点M在直线AB上,则PM长的最小值为$\frac{28}{5}$.
如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-3分别与x轴、y轴交于点A、B,点P的坐标为(0,4).若点M在直线AB上,则PM长的最小值为$\frac{28}{5}$. 一个正方形和两个等边三角形的位置如图所示,若∠1+∠2=100°,则∠3=50°.
一个正方形和两个等边三角形的位置如图所示,若∠1+∠2=100°,则∠3=50°. 某学校教研组对八年级360名学生就“分组合作学习”方式的支持程度进行了调查,随机抽取了若干名学生进行调查,并制作统计图,据此统计图估计该校八年级学生对“分组合作学习”方式非常喜欢和喜欢的人数约为( )
某学校教研组对八年级360名学生就“分组合作学习”方式的支持程度进行了调查,随机抽取了若干名学生进行调查,并制作统计图,据此统计图估计该校八年级学生对“分组合作学习”方式非常喜欢和喜欢的人数约为( )