题目内容
17. 如图所示,折线表示小丽骑车离家的距离与时间的关系,小丽上午九时离开家,下午一五时到家,根据折线图所提供的信息,思考并回答下列问题.
如图所示,折线表示小丽骑车离家的距离与时间的关系,小丽上午九时离开家,下午一五时到家,根据折线图所提供的信息,思考并回答下列问题.(1)小丽什么时间离家最远?离家最远距离是多少?
(2)小丽一共休息了几次?各是从什么时间开始
(3)小丽什么时刻离家的距离是15千米?
分析 (1)根据函数的图象在图中找出到达离家最远的地方的点的坐标即可;
(2)根据函数的图象可得到达C点时,开始第一次休息,在D点时结束休息,求出C、D点的横坐标即可,根据函数的图象可得到达E点时,开始第二次休息,在F点时结束休息,求出E、F点的横坐标即可;
(3)根据函数的图象找出纵坐标为15的点,求出其横坐标即可即可.
解答 解:(1)到达离家最远的地方是12时,离家30km;
(2)他10时30分开始第一次休息,12时开始第二次休息;
(3)设BC解析式为:y=kx+b,可得:
$\left\{\begin{array}{l}{10.5k+b=20}\\{10k+b=10}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=20}\\{b=-190}\end{array}\right.$,
解析式为:y=20x-190,
把y=15代入解析式中可得:15=20x-190,解得:x=10.25;
设回来的解析式为:y=ax+c,可得:
$\left\{\begin{array}{l}{13a+c=30}\\{15a+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-15}\\{c=225}\end{array}\right.$,
解析式为:y=-15x+225,
把y=15代入解析式中可得:15=-15x+225,
解得:x=14.
答:当10时15分和14时时,离家的距离是15千米.
点评 本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.

练习册系列答案
相关题目
8.一个多边形的各内角都是120度,那么它是( )边形.
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
5.下列各式的计算中,正确的是( )
| A. | 8a-4a=4 | B. | 2a2+3a3=5a5 | C. | 5a+3b=8ab | D. | 4x2y-4yx2=0 |
2.从A码头到B码头顺水航行原来需要行驶9小时,现在河道改变取直后,路程近了50千米,而船航行速度每小时增加40千米,结果只需6小时即可到达.若设A、B两码头之间改道后的航程为x千米,则可列方程为( )
| A. | 9(x-40)+50=6x | B. | 9(x-40)-50=6x | C. | $\frac{x+50}{9}$+40=$\frac{x}{6}$ | D. | $\frac{x+50}{9}$-40=$\frac{x}{6}$ |
 如图,在矩形ABCD中,AB=5,BC=13,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则cos∠FBC的值为$\frac{5\sqrt{26}}{26}$.
如图,在矩形ABCD中,AB=5,BC=13,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则cos∠FBC的值为$\frac{5\sqrt{26}}{26}$.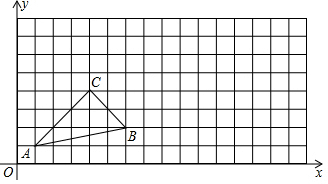 如图,△ABC中顶点A(1,1),B(6,2),C(4,4),将△ABC向右平移5个单位得到△A1B1C1,将△A1B1C1绕点B1顺时针方向旋转90°得到△A2B2C2.
如图,△ABC中顶点A(1,1),B(6,2),C(4,4),将△ABC向右平移5个单位得到△A1B1C1,将△A1B1C1绕点B1顺时针方向旋转90°得到△A2B2C2.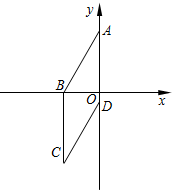 如图,四边形ABCD为菱形,已知A(0,4),B(-3,0).求点D的坐标.
如图,四边形ABCD为菱形,已知A(0,4),B(-3,0).求点D的坐标.