题目内容
如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线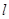 过点A(—1,0),与⊙C相切于点D,求直线
过点A(—1,0),与⊙C相切于点D,求直线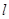 的解析式。
的解析式。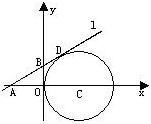
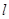 过点A(—1,0),与⊙C相切于点D,求直线
过点A(—1,0),与⊙C相切于点D,求直线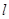 的解析式。
的解析式。
y= x+
x+
 x+
x+
解:如图所示,连接CD, ……………1分
∵直线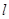 为⊙C的切线,
为⊙C的切线,
∴CD⊥AD。 ……………2分
∵C点坐标为(1,0),
∴OC=1,即⊙C的半径为1,
∴CD=OC=1。 ……………3分
又∵点A的坐标为(—1,0),
∴AC=2,
∴∠CAD=30° ……………4分
作DE⊥AC于E点,则∠CDE=∠CAD=30°
∴CE=
 ……………5分
……………5分
∴OE=OC-CE= ,
,
∴点D的坐标为( ,
, ) ……………6分
) ……………6分
设直线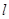 的函数解析式为
的函数解析式为 ……………7分
……………7分
则 ……………8分

解得k= ,b=
,b= ……………9分
……………9分
∴直线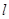 的函数解析式为y=
的函数解析式为y= x+
x+ ……………10分
……………10分
这是一道圆与直角坐标系的综合题,求直线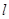 的解析式,通常用待定系数法(知道图象上两个点的坐标即可),题目已给出点A的坐标,再求出一个点即可,抓住点D是直线
的解析式,通常用待定系数法(知道图象上两个点的坐标即可),题目已给出点A的坐标,再求出一个点即可,抓住点D是直线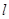 与⊙C的切点,
与⊙C的切点,
由C点坐标为(1,0)及圆的性质易求点D的坐标为( ,
, ),由点A和点D的坐标易求直线
),由点A和点D的坐标易求直线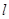 的解析式
的解析式
∵直线
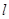 为⊙C的切线,
为⊙C的切线,∴CD⊥AD。 ……………2分
∵C点坐标为(1,0),
∴OC=1,即⊙C的半径为1,
∴CD=OC=1。 ……………3分
又∵点A的坐标为(—1,0),
∴AC=2,
∴∠CAD=30° ……………4分
作DE⊥AC于E点,则∠CDE=∠CAD=30°
∴CE=

 ……………5分
……………5分∴OE=OC-CE=
 ,
,∴点D的坐标为(
 ,
, ) ……………6分
) ……………6分设直线
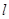 的函数解析式为
的函数解析式为 ……………7分
……………7分则 ……………8分

解得k=
 ,b=
,b= ……………9分
……………9分∴直线
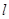 的函数解析式为y=
的函数解析式为y= x+
x+ ……………10分
……………10分这是一道圆与直角坐标系的综合题,求直线
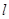 的解析式,通常用待定系数法(知道图象上两个点的坐标即可),题目已给出点A的坐标,再求出一个点即可,抓住点D是直线
的解析式,通常用待定系数法(知道图象上两个点的坐标即可),题目已给出点A的坐标,再求出一个点即可,抓住点D是直线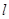 与⊙C的切点,
与⊙C的切点,由C点坐标为(1,0)及圆的性质易求点D的坐标为(
 ,
, ),由点A和点D的坐标易求直线
),由点A和点D的坐标易求直线 的解析式
的解析式
练习册系列答案
相关题目
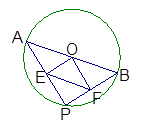

 .
.





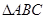 中,AB=" 4" cm,BC="2" cm,
中,AB=" 4" cm,BC="2" cm,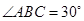 ,把
,把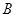 为中心按逆时针方向旋转,使点
为中心按逆时针方向旋转,使点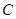 旋转到
旋转到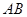 边的延长线上的点
边的延长线上的点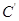 处,那么
处,那么 边扫过的图形(图中阴影部分)的面积是____________ cm2.
边扫过的图形(图中阴影部分)的面积是____________ cm2. 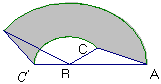
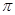 ,则扇形的半径是( )
,则扇形的半径是( ) AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是______.
AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是______.