Question

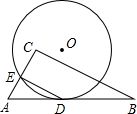△ABC中，∠C=90°，AB切⊙O于D，且DE∥BC，已知AE=，AC=，BC=6，则圆O的半径是________．

Answer 1

分析：延长AC交⊙O于点F，连接DF，由DE∥BC，可知∠AED=∠C=90°，即∠DEF=90°，故可证DF是⊙O的直径，在Rt△ABC中，由勾股定理求AB，由DE∥BC，得△ADE∽△ABC，利用相似比求DE、AD，由切割线定理求AF，在Rt△ADF中，由勾股定理求DF，可证⊙O的半径．
解答：解：延长AC交⊙O于点F，连接DF，
∵DE∥BC，
∴∠DEF=180°-∠ACB=90°，
∴DF是⊙O的直径，
∵AB==，
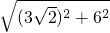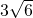DE∥BC，
∴△ADE∽△ABC，则DE：BC=AD：AB=AE：AC
DE：6=AD：=，
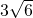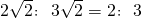∴DE=4，AD=
∵AD是切线∴，
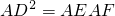∴AF=，
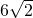∴DF=，
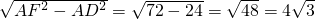⊙O的半径R=．
故答案为：．
点评：本题考查了切线的性质及勾股定理的运用．关键是利用平行线判断FD为直径，灵活运用勾股定理，切割线定理解题．