Question

如图，⊙O的半径为2，弦AB=，点C在弦AB上，AC=AB，则OC的长为________．

Answer 1

分析：过O作OD⊥AB于D，根据垂径定理求出BD，根据勾股定理求出OD，根据勾股定理求出OC即可．
解答：过O作OD⊥AB于D，
∵OD⊥AB，OD过O，AB=，
∴AD=BD=AB=，
∵AB=，点C在弦AB上，AC=AB，
∴AC=，CD=AD-AC=，
在Rt△OBD中，由勾股定理得：OD==1，
在Rt△OCD中，由勾股定理得：OC===，
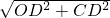故答案为：．
点评：本题考查了初级定理和勾股定理的应用，关键是构造直角三角形，主要考查学生运用定理进行推理和计算的能力．