Question

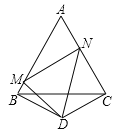
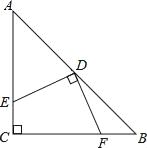
【题目】如图，在△ABC中，AC＝BC＝2，∠C＝90°，D是的中点，DE⊥DF，点E，F分别在AC，BC上，则四边形CFDE的面积为_____．

Answer 1

【答案】1

【解析】

连接CD，证明△ECD≌△FBD，再根据全等三角形的性质和三角形的面积公式解答即可．

连接CD，

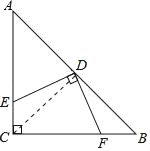
∵∠C＝90°，D是AB的中点，

∴CD＝AB＝BD，

∵AC＝BC，

∴CD⊥AB，∠ACD＝∠B＝45°，

∴∠CDF+∠BDF＝90°，

∵ED⊥DF，

∴∠EDF＝90°，

∴∠EDC+∠CDF＝90°，

∴∠EDC＝∠BDF，

在△ECD与△FBD中

，

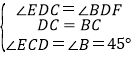∴△ECD≌△FBD（ASA），

∴DE＝DF．

∵在△ABC中，AC＝BC，∠C＝90°，D是AB的中点，

∴S△DCB＝S△ACB＝×2×2×＝1，

∴四边形CFDE的面积S＝S△EDC+S△CDF＝S△BDF+S△CDF＝S△CDB＝1，

故答案为：1.