题目内容
(2012•高邮市一模)电瓶厂投资2000万元安装了电动自行车电瓶流水线,生产的电瓶成本为40元/只,设销售单价为x元(100≤x≤250),年销售量为y万件,年获利为w(万元).经过市场调研发现:当x=100元时,y=20万件.当100<x≤200元时,x在100元的基础上每增加1元,y将减少0.1万件;当200<x≤250元时,x在200元的基础上每增加1元,y将减少0.2万件.(年获利=年销售额-生产成本-投资)
(1)当x=180时,w=
(2)求y与x的函数关系式;
(3)当x为何值时,第一年的年获利亏损最少?
(1)当x=180时,w=
-320
-320
万元;当x=240时,y=2
2
万件;(2)求y与x的函数关系式;
(3)当x为何值时,第一年的年获利亏损最少?
分析:(1)根据:当x=180时,年获利w=(180-40)×销售量-投资2000万元,销售量=[20-(180-100)×0.1],求w的值,当x=240时,先求当x=200时,销售量为10万件,再求当x=240时的销售量;
(2)①当100<x≤200时,根据(1)销售量的求法列出函数式,②当200<x≤300时,先求当x=200时,销售量为10万件,再求出此时销售量的函数关系式;
(3)根据售价分段:①100<x≤200,②200<x≤250,由(2)找出对应的销售量,再根据:年获利w=(x-40)×销售量-投资2000万元,分别列出函数关系式,利用二次函数的性质求最小值.
(2)①当100<x≤200时,根据(1)销售量的求法列出函数式,②当200<x≤300时,先求当x=200时,销售量为10万件,再求出此时销售量的函数关系式;
(3)根据售价分段:①100<x≤200,②200<x≤250,由(2)找出对应的销售量,再根据:年获利w=(x-40)×销售量-投资2000万元,分别列出函数关系式,利用二次函数的性质求最小值.
解答:解:(1)当x=180时,w=(180-40)×[20-(180-100)×0.1]-2000=-320万元;
当x=200时,销售量为[20-(200-100)×0.1]=10万件,
当x=240时,y=[10-(240-200)×0.2]=2万件;
故答案为:-320万元、2万件;
(2)①当100<x≤200时,y=20-0.1(x-100)=-0.1x+30,
②当200<x≤300时,y=10-0.2(x-200)=-0.2x+50,
(先把x=200代入y=-0.1x+30得y=10);
(3)①当100<x≤200时,w=(x-40)(-0.1x+30)-2000=-0.1x2+34x-3200=-0.1(x-170)2-310,
当x=170时,w最大值=-310
②当200<x≤250时,w=(x-40)(-0.2x+50)-2000=-0.2x2+58x-4000=-0.2(x-145)2+205,
∴对称轴是直线x=145,
∵-0.2<0,200<x≤250,
∴在200<x≤250时,w随x的增大而减小,
∵x=200时,w=-400,
∴w最大值<-400,
∴综合①、②可知,当x=170元时,w最大值=-310万元.
当x=200时,销售量为[20-(200-100)×0.1]=10万件,
当x=240时,y=[10-(240-200)×0.2]=2万件;
故答案为:-320万元、2万件;
(2)①当100<x≤200时,y=20-0.1(x-100)=-0.1x+30,
②当200<x≤300时,y=10-0.2(x-200)=-0.2x+50,
(先把x=200代入y=-0.1x+30得y=10);
(3)①当100<x≤200时,w=(x-40)(-0.1x+30)-2000=-0.1x2+34x-3200=-0.1(x-170)2-310,
当x=170时,w最大值=-310
②当200<x≤250时,w=(x-40)(-0.2x+50)-2000=-0.2x2+58x-4000=-0.2(x-145)2+205,
∴对称轴是直线x=145,
∵-0.2<0,200<x≤250,
∴在200<x≤250时,w随x的增大而减小,
∵x=200时,w=-400,
∴w最大值<-400,
∴综合①、②可知,当x=170元时,w最大值=-310万元.
点评:本题考查了一次函数与二次函数的综合运用.关键是理解题意,由题意列出销售量,年利润的函数关系式,注意分段函数的运用.

练习册系列答案
相关题目
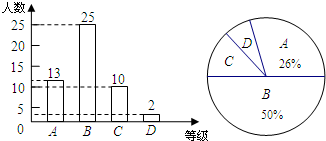 (2012•高邮市一模)学校以1班学生的地理测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成两幅统计图,结合图中信息填空:
(2012•高邮市一模)学校以1班学生的地理测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成两幅统计图,结合图中信息填空: (2012•高邮市一模)如图,DE是△ABC的中位线,M是DE的中点,若△ABC的面积为48cm2,则△DMN的面积为
(2012•高邮市一模)如图,DE是△ABC的中位线,M是DE的中点,若△ABC的面积为48cm2,则△DMN的面积为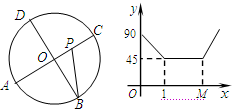 (2012•高邮市一模)如图,A、B、C、D是⊙O四等分点,动点P沿O-C-D-O路线作匀速运动,设运动时间为xs,∠APB=y°,右图表示y与x之间函数关系,则点M的横坐标为
(2012•高邮市一模)如图,A、B、C、D是⊙O四等分点,动点P沿O-C-D-O路线作匀速运动,设运动时间为xs,∠APB=y°,右图表示y与x之间函数关系,则点M的横坐标为