题目内容
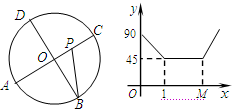 (2012•高邮市一模)如图,A、B、C、D是⊙O四等分点,动点P沿O-C-D-O路线作匀速运动,设运动时间为xs,∠APB=y°,右图表示y与x之间函数关系,则点M的横坐标为
(2012•高邮市一模)如图,A、B、C、D是⊙O四等分点,动点P沿O-C-D-O路线作匀速运动,设运动时间为xs,∠APB=y°,右图表示y与x之间函数关系,则点M的横坐标为| π |
| 2 |
| π |
| 2 |
分析:通过函数图象可以得到函数随自变量的变化规律,通过规律结合图象可以求出关键点C、D的坐标值,从而求出M横坐标的值.
解答:解:根据题意,可知点P从圆心O出发,运动到点C时,∠APB的度数由90°减小到45°,
∴在C点时所对的横坐标为1,
∴OC=1,由弧长公式可以求出弧CD的长度为
π.
当横坐标为M是点P是∠APB由稳定在45°保持不变到增大的转折点;
∴横坐标为M值所对应的点是D点,表示这时P点运动到了D点.
∴M的横坐标=OC+弧CD的长=
π+1.
故答案为:
π+1.
∴在C点时所对的横坐标为1,
∴OC=1,由弧长公式可以求出弧CD的长度为
| 1 |
| 2 |
当横坐标为M是点P是∠APB由稳定在45°保持不变到增大的转折点;
∴横坐标为M值所对应的点是D点,表示这时P点运动到了D点.
∴M的横坐标=OC+弧CD的长=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了动点问题的函数图象,根据速度、路程、时间的关系求出点P在CD弧上运动的时间是解题的关键,有一定难度.

练习册系列答案
相关题目
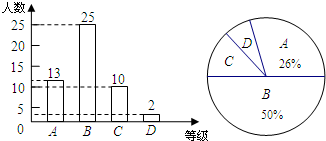 (2012•高邮市一模)学校以1班学生的地理测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成两幅统计图,结合图中信息填空:
(2012•高邮市一模)学校以1班学生的地理测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成两幅统计图,结合图中信息填空: (2012•高邮市一模)如图,DE是△ABC的中位线,M是DE的中点,若△ABC的面积为48cm2,则△DMN的面积为
(2012•高邮市一模)如图,DE是△ABC的中位线,M是DE的中点,若△ABC的面积为48cm2,则△DMN的面积为