题目内容
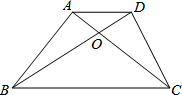 如图,在梯形ABCD中,AD∥BC,AC、BD交于O点AD:BC=3:7,则AO:OC=________,S△AOD:S△BOC=________,S△AOD:S△AOB=________.
如图,在梯形ABCD中,AD∥BC,AC、BD交于O点AD:BC=3:7,则AO:OC=________,S△AOD:S△BOC=________,S△AOD:S△AOB=________.
3:7 9:49 3:7
分析:由条件可以得出△AOD∽△COB,根据相似三角形的性质就可以得出相似三角形的边的关系,面积的关系从而得出结论.
解答:∵AD∥BC,
∴△AOD∽△COB,
∴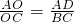 .
. .
.
∵AD:BC=3:7,
∴AO:OC=3:7,S△AOD:S△BOC=9:49.
设△AOD和△DOC中AO和CO边上的高为h,
∴S△AOD= AO•h,S△AOB=
AO•h,S△AOB= CO•h
CO•h
∴S△AOD:S△AOB=AO:CO=3:7.
故答案为:3:7,9:49,3:7.
点评:本题考查了相似三角形的判定与性质的运用,等高的两三角形的底边与面积的关系的运用,解答时求出三角形相似是解答本题的关键.
分析:由条件可以得出△AOD∽△COB,根据相似三角形的性质就可以得出相似三角形的边的关系,面积的关系从而得出结论.
解答:∵AD∥BC,
∴△AOD∽△COB,
∴
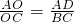 .
. .
.∵AD:BC=3:7,
∴AO:OC=3:7,S△AOD:S△BOC=9:49.
设△AOD和△DOC中AO和CO边上的高为h,
∴S△AOD=
 AO•h,S△AOB=
AO•h,S△AOB= CO•h
CO•h∴S△AOD:S△AOB=AO:CO=3:7.
故答案为:3:7,9:49,3:7.
点评:本题考查了相似三角形的判定与性质的运用,等高的两三角形的底边与面积的关系的运用,解答时求出三角形相似是解答本题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
 11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD
11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10. 如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC.
如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC. 20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=
20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=