题目内容
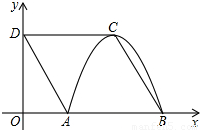
(2010•滨州)如图,四边形ABCD是菱形,点D的坐标是(0, ),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.
),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.(1)求A、B、C三点的坐标;
(2)求过A、B、C三点的抛物线的解析式;
(3)若将上述抛物线沿其对称轴向上平移后恰好过D点,求平移后抛物线的解析式,并指出平移了多少个单位.

【答案】分析:(1)过C作CE⊥AB于E,根据抛物线的对称性知AE=BE;由于四边形ABCD是菱形,易证得△OAD≌△EBC,则OA=AE=BE,可设菱形的边长为2m,则AE=BE=1m,在Rt△BCE中,根据勾股定理即可求出m的值,由此可确定A、B、C三点的坐标;
(2)根据(1)题求得的三点坐标,用待定系数法即可求出抛物线的解析式;
(3)设出平移后的抛物线解析式,将D点坐标代入此函数的解析式中,即可求出平移后的函数解析式,与原二次函数解析式进行比较即可得到平移的单位.
解答: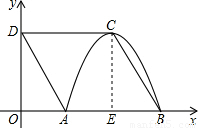 解:(1)过C作CE⊥AB于E,由抛物线的对称性可知AE=BE,
解:(1)过C作CE⊥AB于E,由抛物线的对称性可知AE=BE,
在Rt△AOD和Rt△BEC中,
∵OD=EC,AD=BC,
∴△AOD≌△BEC,
∴OA=BE=AE,(1分)
设菱形的边长为2m,
在Rt△AOD中, ,
,
解得m=1;
∴DC=2,OA=1,OB=3;
∴A、B、C三点的坐标分别为(1,0)、(3,0)、(2, );(4分)
);(4分)
(2)设抛物线的解析式为y=a(x-2)2+ ,
,
代入A点坐标可得a=- ,
,
抛物线的解析式为y=- (x-2)2+
(x-2)2+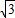 ;(7分)
;(7分)
(3)设抛物线的解析式为y=- (x-2)2+k,
(x-2)2+k,
代入D(0, )可得k=5
)可得k=5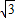 ,
,
所以平移后的抛物线的解析式为y=-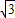 (x-2)2+5
(x-2)2+5 ,(9分)
,(9分)
向上平移了5 -
-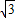 =4
=4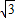 个单位.(10分)
个单位.(10分)
点评:此题考查了菱形的性质、全等三角形的性质、抛物线的对称性、勾股定理以及二次函数图象的平移,综合性较强,难度适中.
(2)根据(1)题求得的三点坐标,用待定系数法即可求出抛物线的解析式;
(3)设出平移后的抛物线解析式,将D点坐标代入此函数的解析式中,即可求出平移后的函数解析式,与原二次函数解析式进行比较即可得到平移的单位.
解答:
 解:(1)过C作CE⊥AB于E,由抛物线的对称性可知AE=BE,
解:(1)过C作CE⊥AB于E,由抛物线的对称性可知AE=BE,在Rt△AOD和Rt△BEC中,
∵OD=EC,AD=BC,
∴△AOD≌△BEC,
∴OA=BE=AE,(1分)
设菱形的边长为2m,
在Rt△AOD中,
 ,
,解得m=1;
∴DC=2,OA=1,OB=3;
∴A、B、C三点的坐标分别为(1,0)、(3,0)、(2,
 );(4分)
);(4分)(2)设抛物线的解析式为y=a(x-2)2+
 ,
,代入A点坐标可得a=-
 ,
,抛物线的解析式为y=-
 (x-2)2+
(x-2)2+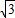 ;(7分)
;(7分)(3)设抛物线的解析式为y=-
 (x-2)2+k,
(x-2)2+k,代入D(0,
 )可得k=5
)可得k=5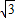 ,
,所以平移后的抛物线的解析式为y=-
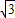 (x-2)2+5
(x-2)2+5 ,(9分)
,(9分)向上平移了5
 -
-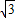 =4
=4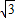 个单位.(10分)
个单位.(10分)点评:此题考查了菱形的性质、全等三角形的性质、抛物线的对称性、勾股定理以及二次函数图象的平移,综合性较强,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
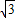 ),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.
),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.