题目内容
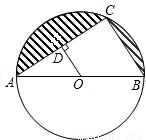
(2010•滨州)如图,已知AB是⊙O的直径,点C在⊙O上,且AB=13,BC=5.(1)求sin∠BAC的值;
(2)如果OD⊥AC,垂足为D,求AD的长;
(3)求图中阴影部分的面积.(精确到0.1)
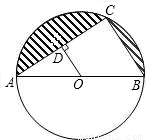
【答案】分析:(1)已知AB是⊙O的直径,则∠ACB=90°,在直角△ABC中根据勾股定理,求出BC,即可得到sin∠BAC的值.
(2)OD⊥AC,则满足垂径定理,因而在直角△ABC中,根据勾股定理就可以求出AD的长.
(3)阴影部分的面积就是半圆的面积减去直角△ABC的面积.
解答:解:(1)∵AB是⊙O的直径,点C在⊙O上,
∴∠ACB=90°.
∵AB=13,BC=5,
∴sin∠BAC= ;
;
(2)在Rt△ABC中,
AC= =
= =12,
=12,
∴AD= AC=6;
AC=6;
(3)S阴影部分= ≈36.3(平方单位).
≈36.3(平方单位).
点评:阴影部分的面积可以看作是半圆的面积减去直角三角形的面积.求不规则的图形的面积,可以转化为几个规则图形的面积的和或差来求.
(2)OD⊥AC,则满足垂径定理,因而在直角△ABC中,根据勾股定理就可以求出AD的长.
(3)阴影部分的面积就是半圆的面积减去直角△ABC的面积.
解答:解:(1)∵AB是⊙O的直径,点C在⊙O上,
∴∠ACB=90°.
∵AB=13,BC=5,
∴sin∠BAC=
 ;
;(2)在Rt△ABC中,
AC=
 =
= =12,
=12,∴AD=
 AC=6;
AC=6;(3)S阴影部分=
 ≈36.3(平方单位).
≈36.3(平方单位).点评:阴影部分的面积可以看作是半圆的面积减去直角三角形的面积.求不规则的图形的面积,可以转化为几个规则图形的面积的和或差来求.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
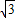 ),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.
),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.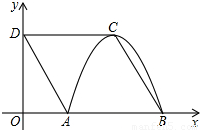
 ),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.
),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.