题目内容
19．已知点P坐标为（1，1），将点P绕原点逆时针旋转45°得点P1，则点P1的坐标为（0，$\sqrt{2}$）．分析 利用点P的坐标特征可判断OP与y轴正方向的夹角为45°，于是可判断点P绕原点逆时针旋转45°得点P1，则点P1在y轴上，根据OP1=OP可得点P1的纵坐标．
解答 
解：如图，连结OP，
∵点P坐标为（1，1），
∴OP与y轴正方向的夹角为45°，
∴点P绕原点逆时针旋转45°得点P1，点P1在y轴上，OP1=OP=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$．
∴点P1的坐标为（0，$\sqrt{2}$）．
故答案为（0，$\sqrt{2}$）．
点评 本题考查了坐标与图形的变化-旋转，熟练掌握旋转变换的性质是解题的关键，作出图形更形象直观．
练习册系列答案
相关题目
10．包装厂有42名工人，每人平均每天可以生产圆形铁片120片或长方形铁片80片．为了每天生产的产品刚好制成一个个密封的圆桶，应该分配多少名工人生产圆形铁片，多少名工人生产长方形铁片？设应分配x名工人生产长方形铁片，（42-x）名工人生产圆形铁片，则下列所列方程正确的是（ ）
| A． | 120x=2×80（42-x） | B． | 80x=120（42-x） | C． | 2×80x=120（42-x） | D． | $\frac{120（42-x）}{80x}=\frac{1}{2}$ |
7．在$\frac{a}{π}$，$\frac{1}{x+1}$，$\frac{1}{5}$x+y，$\frac{{a}^{2}}{a}$，-2x5中．其中是分式的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
14．若|x|=5，|y|=3，则|x-y|等于（ ）
| A． | 2 | B． | ±8 | C． | 8或2 | D． | ±8或±2 |
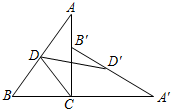如图，将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置，D，D′分别是AB，A′B′的中点，且CD=$\frac{1}{2}AB$，已知AC=8cm，BC=6cm，求线段DD′的长．