题目内容
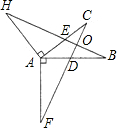 如图,过△ABC的顶点A作AF⊥AB,且AF=AB,再作AH⊥AC,且AH=AC,BH交AC于E,CF交AB于D,BH与CF相交于点O.
如图,过△ABC的顶点A作AF⊥AB,且AF=AB,再作AH⊥AC,且AH=AC,BH交AC于E,CF交AB于D,BH与CF相交于点O.求证:(1)HB=CF;(2)HB⊥CF.
分析:根据已知条件,结合三角形全等的条件可得出△HAB≌△CAF,得到边相等,角相等.再求证HB⊥CF.
解答:解:(1)∵AF⊥AB,AH⊥AC,
∴∠HAC=∠BAF=90°,
∴∠HAC+∠BAC=∠BAF+∠BAC,
即∠BAH=∠CAF.
在△HAB和△CAF中,
∴△HAB≌△CAF(SAS),
∴HB=CF,∠B=∠F.
(2)在△AFD和△BOD中,
∠B=∠F,∠ODB=∠ADF,
∴∠DOB=∠FAD,即HB⊥CF.
∴∠HAC=∠BAF=90°,
∴∠HAC+∠BAC=∠BAF+∠BAC,
即∠BAH=∠CAF.
在△HAB和△CAF中,
|
∴△HAB≌△CAF(SAS),
∴HB=CF,∠B=∠F.
(2)在△AFD和△BOD中,
∠B=∠F,∠ODB=∠ADF,
∴∠DOB=∠FAD,即HB⊥CF.
点评:本题考查了三角形全等的判定和性质;题目较复杂,信息量较大,在解答时要注意仔细读题找出两三角形全等的条件即可解答.

练习册系列答案
相关题目
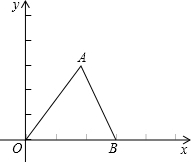 如图,在平面直角坐标系中,已知:△ABC的三个顶点的坐标分别是A(4,6)、B(0,0)、C(6,0).
如图,在平面直角坐标系中,已知:△ABC的三个顶点的坐标分别是A(4,6)、B(0,0)、C(6,0).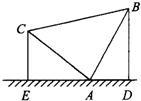 6、把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
6、把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )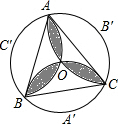 如图,半径为2的正三角形ABC的中心为O,过O与两个顶点画弧,求这三条弧所围成的阴影部分的面积.
如图,半径为2的正三角形ABC的中心为O,过O与两个顶点画弧,求这三条弧所围成的阴影部分的面积.
