题目内容
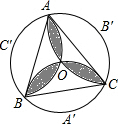如图，半径为2的正三角形ABC的中心为O，过O与两个顶点画弧，求这三条弧所围成的阴影部分的面积．
分析：连接AA′、BB′、CC′，因为△ABC是正三角形，可得到△OAB′也是正三角形；所以一个弓形OA的面积就等于扇形AB′O与△AOB′的面积差．依此计算可求得六个弓形的面积．
解答：
解：连接AA′、BB′、CC′；
∵△ABC是正三角形，
∴△OAB′也是正三角形；
∴S弓形OA=S扇形AB′O-S△AB′O=
-2×
×
=
-
；
所以S阴影=6×（
-
）=4π-6
．
解：连接AA′、BB′、CC′；∵△ABC是正三角形，
∴△OAB′也是正三角形；
∴S弓形OA=S扇形AB′O-S△AB′O=
| 60π×22 |
| 360 |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
| 3 |
所以S阴影=6×（
| 2π |
| 3 |
| 3 |
| 3 |
点评：本题主要考查了扇形面积的计算方法，理清弓形OA的面积计算方法是解题的关键．
练习册系列答案
相关题目
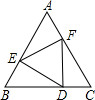如图，边长为n的正△DEF的三个顶点恰好在边长为m的正△ABC的各边上，则△AEF的内切圆半径为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
PC为半径的⊙P与x轴的正半轴交于A、B两点，若抛物线y=ax2+bx+4经过A，B，C三点，且AB=6．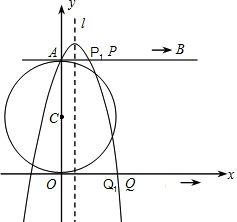
如图，在平面直角坐标系中，以点C（0，4）为圆心，半径为4的圆交y轴正半轴于点A，AB是⊙C的切线．动点P从点A开始沿AB方向以每秒1个单位长度的速度运动，点Q从O点开始沿x轴正方向以每秒4个单位长度的速度运动，且动点P、Q从点A和点O同时出发，设运动时间为t（秒）．
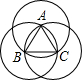如图，边长为1的正△ABC，分别以顶点A，B，C为圆心，1为半径作圆，那么这三个圆所覆盖的图形面积为
（2012•呼和浩特）如图，在一长方形内有对角线长分别为2和3的菱形，边长为1的正六边形和半径为1的圆，则一点随机落在这三个图形内的概率较大的是（ ）