题目内容
某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中AE=MN,准备在形如Rt△AEH的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形MNPQ内种植紫色花草,每种花草的价格如下表:


设AE的长为x米,正方形EFGH的面积为S平方米,买花草所需的费用为W元。解答下列问题:
(1)S与x之间的函数关系式为S=____;
(2)求W与x之间的函数关系式,并求所需的最低费用是多少元?;
(3)当买花草所需的费用最低时,求EM的长。
(1)S与x之间的函数关系式为S=____;
(2)求W与x之间的函数关系式,并求所需的最低费用是多少元?;
(3)当买花草所需的费用最低时,求EM的长。
解:(1)x2+(4-x)2或2x2-8x+16;
(2)W=60×4S△AEH+80(S正方形EFGH-S正方形MNPQ)+120S正方形MNPQ,= +120x2,
+120x2,
=80x2-160x+1280,配方,得
W=80(x-1)2+1200,
∴当x=1时,W最小值=1200,
∴所需的最低费用是1200元;
(3)设EM=a米,则MH=(a+1)米,
在Rt△EMH中,a2+(a+1)2=12+32,解得 ,
,
∵a>0,∴ ,
,
∴EM的长为 米。
米。
(2)W=60×4S△AEH+80(S正方形EFGH-S正方形MNPQ)+120S正方形MNPQ,=
 +120x2,
+120x2,=80x2-160x+1280,配方,得
W=80(x-1)2+1200,
∴当x=1时,W最小值=1200,
∴所需的最低费用是1200元;
(3)设EM=a米,则MH=(a+1)米,
在Rt△EMH中,a2+(a+1)2=12+32,解得
 ,
,∵a>0,∴
 ,
,∴EM的长为
 米。
米。
练习册系列答案
相关题目
某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中AE=MN.准备在形如Rt△MEH的四个全等三角形内种植黄色花草,在形如Rt△AEH的四个全等三角形内种植红色花草,在正方形MNPQ内种植紫色花草,每种花草的价格如下表:
设AE的长为x米,正方形EFGH的面积为S平方米,买花草所需的费用为W元,解答下列问题:
(1)S与x之间的函数关系式为S= ;
(2)求W与x之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求EM的长.
| 品 种 | 红色花草 | 黄色花草 | 紫色花草 |
| 价格(元/米2) | 60 | 80 | 120 |

(1)S与x之间的函数关系式为S=
(2)求W与x之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求EM的长.
某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中![]() .准备在形如Rt
.准备在形如Rt![]() 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形![]() 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:
| 品种 | 红色花草 | 黄色花草 | 紫色花草 |
| 价格(元/米2) | 60 | 80 | 120 |
设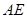 的长为
的长为![]() 米,正方形
米,正方形![]() 的面积为
的面积为![]() 平方米,买花草所需的费用为
平方米,买花草所需的费用为![]() 元,解答下列问题:
元,解答下列问题:
(1)![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() ;
;
(2)求![]() 与
与![]() 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求![]() 的长.
的长.

某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中 .准备在形如Rt
.准备在形如Rt 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:
设 的长为
的长为 米,正方形
米,正方形 的面积为
的面积为 平方米,买花草所需的费用为
平方米,买花草所需的费用为 元,解答下列问题:
元,解答下列问题:
(1) 与
与 之间的函数关系式为
之间的函数关系式为 ;
;
(2)求 与
与 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求 的长.
的长.

 .准备在形如Rt
.准备在形如Rt 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:| 品种 | 红色花草 | 黄色花草 | 紫色花草 |
| 价格(元/米2) | 60 | 80 | 120 |
 的长为
的长为 米,正方形
米,正方形 的面积为
的面积为 平方米,买花草所需的费用为
平方米,买花草所需的费用为 元,解答下列问题:
元,解答下列问题:(1)
 与
与 之间的函数关系式为
之间的函数关系式为 ;
;(2)求
 与
与 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;(3)当买花草所需的费用最低时,求
 的长.
的长.
某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中 .准备在形如Rt
.准备在形如Rt 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:
| 品种 | 红色花草 | 黄色花草 | 紫色花草 |
| 价格(元/米2) | 60 | 80 | 120 |
 的长为
的长为 米,正方形
米,正方形 的面积为
的面积为 平方米,买花草所需的费用为
平方米,买花草所需的费用为 元,解答下列问题:
元,解答下列问题:(1)
 与
与 之间的函数关系式为
之间的函数关系式为 ;
;(2)求
 与
与 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;(3)当买花草所需的费用最低时,求
 的长.
的长.
某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中 .准备在形如Rt
.准备在形如Rt 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:
|
品种 |
红色花草 |
黄色花草 |
紫色花草 |
|
价格(元/米2) |
60 |
80 |
120 |
设 的长为
的长为 米,正方形
米,正方形 的面积为
的面积为 平方米,买花草所需的费用为
平方米,买花草所需的费用为 元,解答下列问题:
元,解答下列问题:
(1) 与
与 之间的函数关系式为
之间的函数关系式为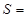 ;
;
(2)求 与
与 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求 的长.
的长.
