题目内容
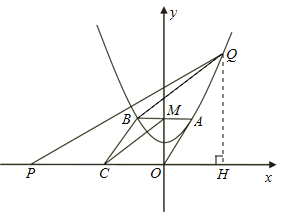
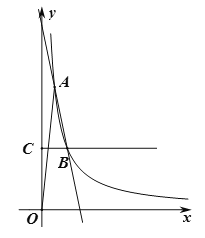
【题目】如图，在平面直角坐标系
中，一抛物线的顶点坐标是
，且过点
，平行四边形
的顶点在
此抛物线上，
与
轴相交于点
.己知点
的坐标是
，点
是抛物线上任意一点.
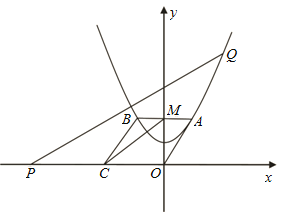
（1）求此抛物线的解析式及点的坐标；
（2）在抛物线上是否存在点
，使得
的面积是
的面积的2倍？若存在，求此时点的坐标.
（3）在
轴上有一动点
，若
，试建立
关于的函数解析式，并求出
的运动范围；
【答案】（1）y=
x2+1；M（0，2）；（2）存在，Q（2
，4）或（-2，4）；（3）t=
，点P的运动范围为x轴上（
，0）及其左侧的部分
【解析】
（1）由抛物线的顶点坐标是（0，1），且过点（-2，2），故设其解析式为y=ax2+1，则利用待定系数法即可求得此抛物线的解析式，又由四边形OABC是平行四边形，则可求得点A与M的坐标；
（2）设△ABQ的边AB上的高为h，可得S△BCM=
BMOM=2，则又由S△ABQ=2S△BCM=AB×h，即可求得点Q的坐标；
（3）作QH⊥x轴，交x轴于点H，即可证得△PQH∽△CMO，根据相似三角形的对应边成比例，即可求得x与t的关系式，求出t的取值范围，从而确定点P的运动范围.
解：（1）∵抛物线的顶点坐标是（0，1），且过点（-2，2），
故设其解析式为y=ax2+1，
则有：2=（-2）2×a+1，
得a=，
∴此抛物线的解析式为：y=x2+1，
∵四边形OABC是平行四边形，
∴AB=OC=4，AB∥OC，
又∵y轴是抛物线的对称轴，
∴点A与B是抛物线上关于y轴的对称点，
则MA=MB=2，
即点A的横坐标是2，
则其纵坐标y=×22+1=2，
即点A（2，2），
故点M（0，2）；
（2）设△ABQ的边AB上的高为h，
∵S△BCM=BMOM=2，
∴S△ABQ=2S△BCM=AB×h=4，
∴h=2，
∴点Q的纵坐标为4，代入y=x2+1，
得x=±2，
∴存在符合条件的点Q，其坐标为（2，4），（-2/span>，4）；
（3）作QH⊥x轴，交x轴于点H．
则∠QHP=∠MOC=90°，
∵PQ∥CM，
∴∠QPH=∠MCO，
∴△PQH∽△CMO，
∴
，
即
，
而y=x2+1，
∴
，
∴t=，
∴t的取值范围是：t≤，
∴点P的运动范围为x轴上（，0）及其左侧的部分.
