Question

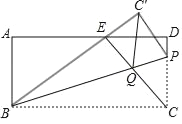
【题目】如图，在矩形ABCD中，AB＝6，P为边CD上一点，把△BCP沿直线BP折叠，顶点C折叠到C'，连接BC'与AD交于点E，连接CE与BP交于点Q，若CE⊥BE．

（1）求证：△ABE∽△DEC；

（2）当AD＝13时，AE＜DE，求CE的长；

（3）连接C'Q，直接写出四边形C'QCP的形状：　 　．当CP＝4时，并求CEEQ的值．

Answer 1

【答案】(1)见解析；（2）CE＝；（3）菱形，理由见解析

【解析】

（1）由题意可得∠AEB+∠CED=90°，且∠ECD+∠CED=90°，可得∠AEB=∠ECD，且∠A=∠D=90°，则可证△ABE∽△DEC；

（2）设AE=x，则DE=13-x，由相似三角形的性质可得，即：，可求x的值，即可得DE=9，根据勾股定理可求CE的长；

（3）由折叠的性质可得CP=C'P，CQ=C'Q，∠C'PQ=∠CPQ，∠BC'P=∠BCP=90°，由平行线的性质可得∠C'PQ=∠CQP=∠CPQ，即可得CQ=CP=C'Q=C'P，则四边形C'QCP是菱形，通过证△C'EQ∽△EDC，可得，即可求CEEQ的值．

（1）∵CE⊥BE，

∴∠BEC＝90°，

∴∠AEB+∠CED＝90°，

又∵∠ECD+∠CED＝90°，

∴∠AEB＝∠ECD，

又∵∠A＝∠D＝90°，

∴△ABE∽△DEC；

（2）设AE＝x，则DE＝13﹣x，

由（1）知：△ABE∽△DEC，

∴，即：，

∴x2﹣13x+36＝0，

∴x1＝4，x2＝9，

又∵AE＜DE，

∴AE＝4，DE＝9，

在Rt△CDE中，由勾股定理得：；

（3）∵折叠，

∴CP＝C'P，CQ＝C'Q，∠C'PQ＝∠CPQ，∠BC'P＝∠BCP＝90°，

∵CE⊥BC'，∠BC'P＝90°，

∴CE∥C'P，

∴∠C'PQ＝∠CQP，

∴∠CQP＝∠CPQ，

∴CQ＝CP，

∴CQ＝CP＝C'Q＝C'P，

∴四边形C'QCP是菱形，

故答案为：菱形；

∵四边形C'QCP是菱形，

∴C'Q∥CP，C'Q＝CP，∠EQC'＝∠ECD

又∵∠C'EQ＝∠D＝90°

∴△C'EQ∽△EDC

∴，

即：CEEQ＝DCC'Q＝6×4＝24.