题目内容
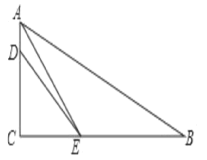
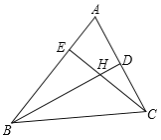
【题目】如图,在△ABC 中,记∠A=x 度,回答下列问题:
(1)图中共有三角形 个.
(2)若 BD,CE 为△ABC 的角平分线,则∠BHC= 度(结果用含 x 的代数式
表示),并证明你的结论.
(3)若 BD,CE 为△ABC 的高线,则∠BHC= 度(结果用含 x 的代数式表示),并证明你的结论.
【答案】(1)图中共有三角形 8 个;(2)(90+ ![]() x ) ;(3)(180-x).
x ) ;(3)(180-x).
【解析】
本题考查的是三角形内角和定理,分析题意观察图形,根据三角形内角和为180°可知∠ABC=![]() ,根据角平分线的性质可以求出∠BHC,根据高线的性质可知∠CDB=∠BEC=90,再次利用三角形内角和定理可以求答案
,根据角平分线的性质可以求出∠BHC,根据高线的性质可知∠CDB=∠BEC=90,再次利用三角形内角和定理可以求答案
解:(1)图中共有三角形 8 个;
(2)∠BHC=(90+ ![]() )度.
)度.
∵BD,CE 分别是∠ABC,∠ACB 的平分线,
∴∠BHC=180-∠HBC-∠HCB=180-![]() (∠ABC+∠ACB)= (90+
(∠ABC+∠ACB)= (90+ ![]() )度.
)度.
(3)∠BHC=(180-x)度,
∵BD,CE 为△ABC 的高线,
∴BD⊥AC,CE⊥AB,
∴∠CDB=∠BEC=90,
∵∠BEC+∠ABC+∠BCH=180°
∠CDB+∠ACB+∠CBH=180°
∴∠BEC+∠ABC+∠BCH+∠CDB+∠ACB+∠CBH=360°
∠ABC+∠BCH+∠ACB+∠CBH=180°
∵∠ABC+∠ACB=180°-∠A
∠BCH+∠CBH=180°-∠BHC
∴180°-∠A+180°-∠BHC=180°
∴∠BHC=(180-x)度

练习册系列答案
相关题目