题目内容
计算：
（1）（a+3）2+a（2-a）
（2）（a+b）2（a-b）2-（a-b）（a+b）（a2+b2）
（3）a（a-2b）+2（a+b）（a-b）+（a+b）2．
（1）（a+3）2+a（2-a）
（2）（a+b）2（a-b）2-（a-b）（a+b）（a2+b2）
（3）a（a-2b）+2（a+b）（a-b）+（a+b）2．
考点：整式的混合运算
专题：
分析：（1）按先乘方后乘除的顺序运算即可，
（2）先利用平方差，再提取公因式求解即可，
（3）运用先乘方后乘除的顺序运算即可．
（2）先利用平方差，再提取公因式求解即可，
（3）运用先乘方后乘除的顺序运算即可．
解答：解：（1）（a+3）2+a（2-a）
=a2+6a+9+2a-a2
=8a+9，
（2）（a+b）2（a-b）2-（a-b）（a+b）（a2+b2）
=（a2-b2）2-（a2-b2）（a2+b2）
=（a2-b2）（a2-b2-a2-b2）
=-2a2b2+2b4；
（3）a（a-2b）+2（a+b）（a-b）+（a+b）2
=a2-2ab+2a2-2b2+a2+2ab+b2
=4a2-b2．
=a2+6a+9+2a-a2
=8a+9，
（2）（a+b）2（a-b）2-（a-b）（a+b）（a2+b2）
=（a2-b2）2-（a2-b2）（a2+b2）
=（a2-b2）（a2-b2-a2-b2）
=-2a2b2+2b4；
（3）a（a-2b）+2（a+b）（a-b）+（a+b）2
=a2-2ab+2a2-2b2+a2+2ab+b2
=4a2-b2．
点评：本题主要考查了有乘方、乘除的混合，解题的关键是熟记平方差及完全平方公式．
练习册系列答案
优生乐园系列答案
相关题目
如图在Rt△ABC中，∠ACB=90°，CD⊥AB于D．
如图，在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，分别交AB、AC于点D、E．若AB=5，AC=3，则△ADE的周长是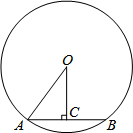
如图，AB是⊙O的弦，OC⊥AB于点C，连接OA，AB=12，⊙O半径为10．
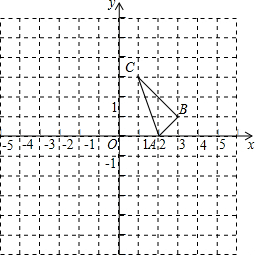如图所示的正方形网格中，△ABC的顶点均在格点上，在所给平面直角坐标系中解答下列问题：
如图，半径为5的⊙A中，弦BC，ED所对的圆心角分别是∠BAC，∠EAD．已知DE=6，∠BAC+∠EAD=180°，则弦BC的弦心距等于